vektor i plan
Behöver hjälp med att komma igång med en uppgift
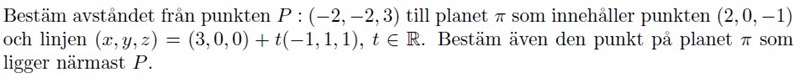
Finns det något särskilt sätt som man hittar avståndet till ett plan.
Nån som vet vad jag ska söka på eller kan hjälpa mig visa hur man gör?
Tack!
börja med att bestämma planets ekvation
Okej, jag kan få planets ekvation utifrpn tre punker. Ska jag se
som mina tre punkter i planet?
välj ett värde för t så blir det lättare
vilket värde som helst? t=1?
Du måste använda hela linjen tillsammans med t
fick planets ekvation:
17x-23y+13z=31
När jag gjorde t=1 i:
p3=t(−1,1,1) .
Vad menar du med hela linjen tillsamans med t?
vad är skillnaden mellan
(3,0,0)+t(-1,1,1) och t(-1,1,1)
(3,0,0). Vad menas?
den ena är en linje som går genom origo. den andra är en linje som går genom punkten (3,0,0). det är inte samma sak.
p1=(2,0,-1)
p2=(3,0,0)
p3=(3,0,0)+1(-1,1,1)=(2,1,1)
Okej då fick jag det såhär

Alltså planets ekvation blir . Så långt rätt den här gången hahah?
edit: såg nu att det va fel
En normal till planet är . En punkt i planet ges av . Avståndet till punkten är alltså
Tack så mycket för hjälpen!