Vektorer

I detta fallet ser du i bilden att $\bar{u}$ och $\bar{v}$ är riktade åt motsatt håll.

Vektorns riktning "ingår" i storheten $\bar{v}$ , så vektorsumman skrivs $\bar{u}+\bar{v}$ är rätt.

Vektorn $\bar{u}-\bar{v}$ (vilket är samma sak som $\bar{u}+(-1)\cdot\bar{v}$) är en helt annan vektor än den som visas i boken.

Jämför med "vanliga" tal:

Om till exempel $a = 5$ och $b = -3$ så "ingår" minustecknet i den obekanta storheten $b$ och därför blir $a+b = 2$.

Storheten $a - b$ (vilket är samma sak som $a + (-1)\cdot b$) har ett helt annat värde, nämligen $8$.

------------

Om du inte redan har stött på det tidigare så kommer du lite senare att se att vektorer kan beskrivas i koordinatform och då kommer du att kunna beräkna deras riktning algebraiskt.

Beskrivning av polygonmetoden

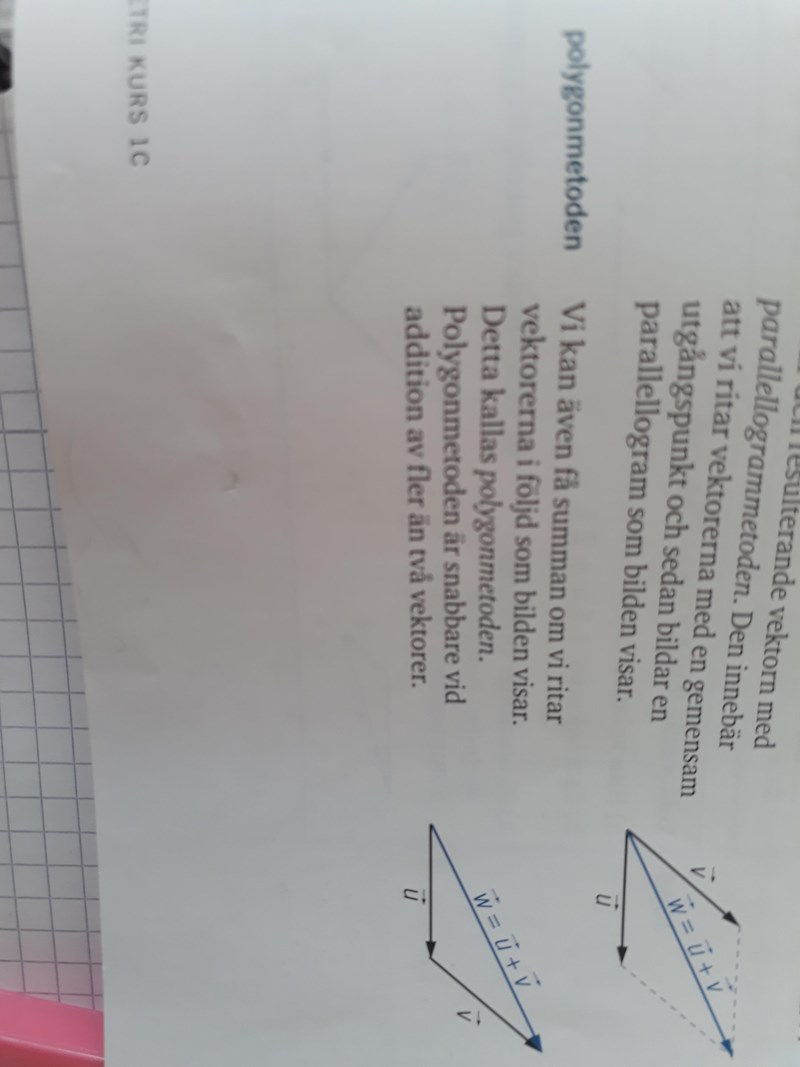På uppgiften jag visade så ritar man inte vektorerna i följd men det räknas ändå som polygonmetoden? 

Egentligen inte.

Egentligen borde de ha ritat som jag gjort i bilden nedan men sedan förklarat att de parallellförskjutit ena vektorn för tydlighets skull.

Jaa, de ska alltså i teorin vara målade på varandra, "Följa" fast åt andra hållet, men de målas separat? Knepigt, men tror jag fattar!

Ja polygonmetoden för addition går ut på att vektorerna "sätts ihop" som ett tåg.

För att konstruera $\bar{a}+\bar{b}$ sätter man starten av $\bar{b}$ i samma punkt som spetsen (slutet) av $\bar{a}$.