Vektorer i två delrum

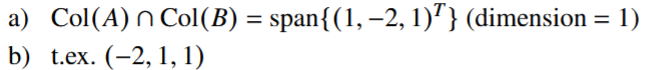
u ligger i Col(A) omm det finns någon vektor x i R² sådan att u = Ax.

Pss om u ligger Col(B) så måste det finnas en vektor y i R² sådan att u = By.

Omvänt om vi har vektorer x och y sådana att Ax = By så ligger u = Ax = By i Col(A)$\cap$Col(B).

Sedan gäller det generellt att snittet av två delrum är ett delrum.

Lös ekvationen Ax = By. Vilket kan skrivas om till matrisekvationen

$\left[\begin{array}{cc}A& -B\end{array}\right]\left[\begin{array}{c}\mathit{x}\\ \mathit{y}\end{array}\right]$=0.

Kommer du vidare?

PATENTERAMERA skrev:

Lös ekvationen Ax = By. Vilket kan skrivas om till matrisekvationen

$\left[\begin{array}{cc}A& -B\end{array}\right]\left[\begin{array}{c}\mathit{x}\\ \mathit{y}\end{array}\right]$=0.

Kommer du vidare?

Får jag inte då att x och y blir = 0? Hur visar det vilka vektorer som ligger i både Col(A) och Col(B)?

Det är bara en möjlig lösning. Det finns flera.

Är du med på att u $\in Col\left(A\right)\cap Col\left(B\right)$ om och endast om det existerar x, y $\in {\mathrm{ℝ}}^2$ sådana att u = Ax = By?

col(A) och col(B) är bara helt vanliga plan i R3. Vektorerna som spänner upp planen har du redan givna. Beräknar du skärningen mellan planen så får du svaret på a. Det enda du behöver göra är gauss elimination.