Vektorfält och kurvintegraler
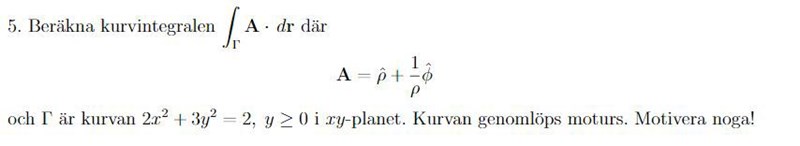

Jag missar något vid parametriseringen. Mer specifikt, givet vektorfältet och den parametriserade ortsvektorn, hur blir ?
Obs, termen försvinner eftersom att på
Om man tar ett annat exempel i kartesiska koordinater, så fungerar ju insättning av funktioner i vektorfält så här
Således borde ju insättningen i uppgiften på bilden ge
Är det någon som kan förklara var jag tänker fel?
Din sista beräkning i kartesiska koordinater är ett mysterium för mig. Hur får du att vektorfältet är ?
Frågar du mig blir det bara en massa krångel om man ska omvandla till kartesiska koordinater.
AlvinB skrev:Din sista beräkning i kartesiska koordinater är ett mysterium för mig. Hur får du att vektorfältet är ?
Frågar du mig blir det bara en massa krångel om man ska omvandla till kartesiska koordinater.
Oj där var jag väldigt otydlig. Exemplet med vektorfältet är helt orelaterat till uppgiften på bilden. Jag försökte bara illustrera vad det är jag inte förstår med ett enkelt exempel i kartesiska koordinater.
Jag har nu redigerat inlägget för att tydliggöra.
Vad är vektorfältet ? Det står varken i uppgiftens text eller i dess lösning.
Sedan bör det tydliggöras om det är cylinderkoordinater som används och om vektorfältet är tredimensionellt?
Albiki skrev:Vad är vektorfältet ? Det står varken i uppgiftens text eller i dess lösning.
Sedan bör det tydliggöras om det är cylinderkoordinater som används och om vektorfältet är tredimensionellt?
var bara ett exempel jag använde för att illustrera det jag inte förstod.
är tredimensionellt och beskrivs med cylinderkoordinaterna .
Cirice skrev:AlvinB skrev:Din sista beräkning i kartesiska koordinater är ett mysterium för mig. Hur får du att vektorfältet är ?
Frågar du mig blir det bara en massa krångel om man ska omvandla till kartesiska koordinater.
Oj där var jag väldigt otydlig. Exemplet med vektorfältet är helt orelaterat till uppgiften på bilden. Jag försökte bara illustrera vad det är jag inte förstår med ett enkelt exempel i kartesiska koordinater.
Jag har nu redigerat inlägget för att tydliggöra.
Nu är jag ännu mer förvirrad.
Du har vektorfältet som tar en tredimensionell vektor och ger en tredimensionell vektor ; båda vektorer uttryckta i kartesiska koordinater.
Sedan tar en tvådimensionell vektor och ger en endimensionell vektor (ett tal) .
Sedan vill du att ska ta den endimensionella vektorn och ge en endimensionell vektor .
Förstår du att detta är nonsens?
Albiki skrev:Cirice skrev:AlvinB skrev:Din sista beräkning i kartesiska koordinater är ett mysterium för mig. Hur får du att vektorfältet är ?
Frågar du mig blir det bara en massa krångel om man ska omvandla till kartesiska koordinater.
Oj där var jag väldigt otydlig. Exemplet med vektorfältet är helt orelaterat till uppgiften på bilden. Jag försökte bara illustrera vad det är jag inte förstår med ett enkelt exempel i kartesiska koordinater.
Jag har nu redigerat inlägget för att tydliggöra.
Nu är jag ännu mer förvirrad.
Du har vektorfältet som tar en tredimensionell vektor och ger en tredimensionell vektor ; båda vektorer uttryckta i kartesiska koordinater.
Sedan tar en tvådimensionell vektor och ger en endimensionell vektor (ett tal) .
Sedan vill du att ska ta den endimensionella vektorn och ge en endimensionell vektor .
Förstår du att detta är nonsens?
Nej, jag förstår faktiskt inte varför det är nonsens. Det är väl ekvivalent med att parametrisera en linje och sedan låta vektorfältet verka på linjen?
Albiki skrev:[...]
Nu är jag ännu mer förvirrad.
Du har vektorfältet som tar en tredimensionell vektor och ger en tredimensionell vektor ; båda vektorer uttryckta i kartesiska koordinater.
Sedan tar en tvådimensionell vektor och ger en endimensionell vektor (ett tal) .
Sedan vill du att ska ta den endimensionella vektorn och ge en endimensionell vektor .
Förstår du att detta är nonsens?
Jag tror att Cirice egentligen menar att ska ta en skalär och ge en tredimensionell vektor, d.v.s. en parametrisering och att detta sedan med insättning i vektorfältet blir . Dock är detta fält bara en avbildning som ger ut samma utvärden som invärden och är därför ett ganska trivialt exempel.
För att återgå till ursprungsuppgiften:
Jag förstår det som att du har svårigheter att begripa varför . Vi har fältet :
och parametriseringen
För att få fram tar vi helt enkelt -komponenten från och sätter in den i vektorfältet:
Det är två saker som är viktiga att förstå
- -komponenten i vektorfältet är konstant. Den kommer att vara oavsett vad man stoppar in.
- -komponenten i vektorfältet beror på . Eftersom vi i parametriseringen har -komponenten sätter vi in .
AlvinB skrev:Albiki skrev:[...]
Nu är jag ännu mer förvirrad.
Du har vektorfältet som tar en tredimensionell vektor och ger en tredimensionell vektor ; båda vektorer uttryckta i kartesiska koordinater.
Sedan tar en tvådimensionell vektor och ger en endimensionell vektor (ett tal) .
Sedan vill du att ska ta den endimensionella vektorn och ge en endimensionell vektor .
Förstår du att detta är nonsens?
Jag tror att Cirice egentligen menar att ska ta en skalär och ge en tredimensionell vektor, d.v.s. en parametrisering och att detta sedan med insättning i vektorfältet blir . Dock är detta fält bara en avbildning som ger ut samma utvärden som invärden och är därför ett ganska trivialt exempel.
För att återgå till ursprungsuppgiften:
Jag förstår det som att du har svårigheter att begripa varför . Vi har fältet :
och parametriseringen
För att få fram tar vi helt enkelt -komponenten från och sätter in den i vektorfältet:
Det är två saker som är viktiga att förstå
- -komponenten i vektorfältet är konstant. Den kommer att vara oavsett vad man stoppar in.
- -komponenten i vektorfältet beror på . Eftersom vi i parametriseringen har -komponenten sätter vi in .
Precis! Jag var visst slarvig med notationen.
Tack för en tydlig förklaring. Känns ganska uppenbart att det måste bli så nu
Tack även till Albiki för att du tog dig tid att försöka förstå mig.


