Vektorprodukt Mekanik
Hej!
Jag har ett par frågor gällande bilden nedan. 1) jag förstår ej hur man använder högerhandsregel för att bestämma riktningen som bilden visar med tummen upp och fingrar. Är tummen alltså kryssprodukten för en vektor a×b ? Långfingret är vektorn b och lillfingret är vektor a? Hur definierar vi positiv riktning och negativ riktning?
2) varför är det -b×a där det står a×b=-b×a?
Ser du den krökta pilen i figuren? Det är tänkt att du kröker fingrarna så att de följer den krökta pilen från a till b. När du beräknar b x a så skall du tänka dig en liknande krökt pil som går från b till a i stället och kröka fingrarna längs denna pil. Det kan du dock endast göra om din tumme pekar åt andra hållet (testa själv) och därför blir kryssprodukten b x a motriktad kryssprodukten a x b.
PATENTERAMERA skrev:Ser du den krökta pilen i figuren? Det är tänkt att du kröker fingrarna så att de följer den krökta pilen från a till b. När du beräknar b x a så skall du tänka dig en liknande krökt pil som går från b till a i stället och kröka fingrarna längs denna pil. Det kan du dock endast göra om din tumme pekar åt andra hållet (testa själv) och därför blir kryssprodukten b x a motriktad kryssprodukten a x b.
Hm nej jag ser ej krökta pilen du pratar om och förstår ej hur du menar med tummen.
Det står precis bredvid den krökta pilen.
destiny99 skrev:PATENTERAMERA skrev:Ser du den krökta pilen i figuren? Det är tänkt att du kröker fingrarna så att de följer den krökta pilen från a till b. När du beräknar b x a så skall du tänka dig en liknande krökt pil som går från b till a i stället och kröka fingrarna längs denna pil. Det kan du dock endast göra om din tumme pekar åt andra hållet (testa själv) och därför blir kryssprodukten b x a motriktad kryssprodukten a x b.
Hm nej jag ser ej krökta pilen du pratar om och förstår ej hur du menar med tummen.
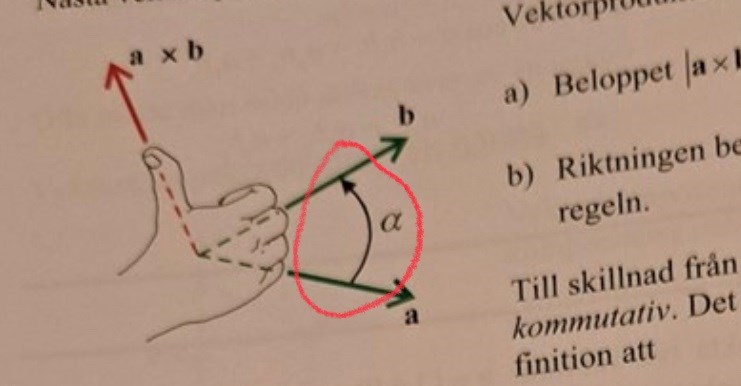
Jag tycker att bilden är jättedålig. Har författaren till boken verkligen förstått högerhandsregeln?
Tumme (a), pekfinger (b) och långfinger (a x b) på högerhanden bildar axlarna i ett vanligt högerortonormerat system, om man håller handen rätt.
Det finns två olika sätt att illustrera riktningen på en kryssprodukt.
Det ena är med krökta fingrar, det andra är med spretande pek- och långfinger.
I båda fallen pekar tummen ut kryssproduktens riktning.
I uppgiften används den förstnämnda och därför står det ingenting om pek- eller långfinger.
Vad jag vet så har de två metoderna tyvärr samma namn, nämligen högerhandsregeln.
Jag tycker det här med spretande fingrar är mest praktiskt i fysik, där riktningarna har specifika betydelser: tummen är stark så det är kraften, pekfingret pekar ut rörelseriktningen. Jag tänker alltså på F = q v x B. Och nu inser jag att då måste man i alla fall ha koll på kryssproduktregeln separat, eller komma ihåg att det är v x B, och inte B x v.
För att komma ihåg kryssprodukt skulle den regeln inte hjälpa mig alls. Jag brukar inte använda någon fingerregel för kryssprodukt, utan bara tänka på att i x j = k, dvs. kryssprodukten av x-riktningen med y-riktningen är z-riktningen, sedan ger sig resten.
Asså jag har lärt mig hur man räknar fram tex ey mha kryssproduktregeln(se bild nedan) eller som determinant och tänker ej på högerhandsregeln.
Du behöver skapa dig en egen minnesregel för att förstå hur , och förhåller sig till varandra i uttrycket . Man måste inte använda höger hand. Eller någon hand alls. Det viktiga är att ha något att "haka upp kunskapen på" så att man slipper beräkna en determinant så fort man stöter på en kryssprodukt. Själv använder jag ungefär som Laguna att i ett högerorienterat koordinatsystem. Jag tänker mig att "roterar moturs mot" och ger .
En lag från fysiken du kanske redan lärt dig är "BIL-formeln",
Notera ordningen på och åt vilket håll vektorerna pekar nedan och vilken hand som används. Försäkra dig om att du lika gärna kan använda höger hand men att du då måste byta uppräkningsordning på fingrarna.

D4NIEL skrev:Du behöver skapa dig en egen minnesregel för att förstå hur , och förhåller sig till varandra i uttrycket . Man måste inte använda höger hand. Eller någon hand alls. Det viktiga är att ha något att "haka upp kunskapen på" så att man slipper beräkna en determinant så fort man stöter på en kryssprodukt. Själv använder jag ungefär som Laguna att i ett högerorienterat koordinatsystem. Jag tänker mig att "roterar moturs mot" och ger .
En lag från fysiken du kanske redan lärt dig är "BIL-formeln",
Notera ordningen på och åt vilket håll vektorerna pekar nedan och vilken hand som används. Försäkra dig om att du lika gärna kan använda höger hand men att du då måste byta uppräkningsordning på fingrarna.
Tyvärr har jag ingen minnesregel då jag räknar tex determinanten eller memorerar som de skriver i kursboken ex×ez=-ey osv
Som D4NIEL säger så måste du lära dig någon form av högerhandsregeln för kryssprodukten, eftersom det är viktigt att förstå kryssproduktens geometriska betydelse.
Notera att formeln med determinanten gäller då ex, ey och ez är en ortonormerad högerhandsbas. För generella basvektorer blir formeln lite mer komplicerad, men det brukar inte läras ut i moderna läroböcker - du får kolla böcker från 60-talet, typ.
PATENTERAMERA skrev:måste du lära dig någon form av högerhandsregeln för kryssprodukten
Det brukar räcka med att veta att Och determinantformeln.
Pieter Kuiper skrev:PATENTERAMERA skrev:måste du lära dig någon form av högerhandsregeln för kryssprodukten
Det brukar räcka med att veta att Och determinantformeln.
Varför är det ett minustecken framför b och varför är det lika med b×a? Är det omvänd kryssprodukten?
destiny99 skrev:Varför är det ett minustecken framför b
Enligt definition, se din bok:
destiny99 skrev:Pieter Kuiper skrev:PATENTERAMERA skrev:måste du lära dig någon form av högerhandsregeln för kryssprodukten
Det brukar räcka med att veta att Och determinantformeln.
Varför är det ett minustecken framför b och varför är det lika med b×a? Är det omvänd kryssprodukten?
Beviset för att a x b = -b x a vid vektorprodukt är baserat på definitionen av vektorprodukten. Anta att vi har vektorerna a = [a1, a2, a3] och b = [b1, b2, b3]. Vektorprodukten av a och b, a x b, är definierad som [a2 * b3 - a3 * b2, a3 * b1 - a1 * b3, a1 * b2 - a2 * b1] (se boken)
Om vi nu beräknar b x a, vi får [b2 * a3 - b3 * a2, b3 * a1 - b1 * a3, b1 * a2 - b2 * a1]. Som du kan se, detta är exakt det negativa av a x b, och så a x b = -b x a.
Definitionen av vektorprodukten i mekanikboken är ju rent geometrisk. Och från den definitionen är det ganska klart, med utnyttjande av högerhandsregeln, att a x b = -(b x a).
Den formel som du använder måste, om man vill vara stringent, först härledas från definitionen. Bokens härledning är dessutom lite fusk, eftersom man utnyttjar algebraiska egenskaper hos kryssprodukten som inte först bevisats gälla med utgångspunkt från bokens geometriska definition, detta är inte helt trivialt att göra.
PATENTERAMERA skrev:Bokens härledning är dessutom lite fusk, eftersom man utnyttjar algebraiska egenskaper hos kryssprodukten som inte först bevisats gälla med utgångspunkt från bokens geometriska definition, detta är inte helt trivialt att göra.
Jag förstår inte, vilka algebraiska egenskaper menar du? Definitionen innehåller bara två geometriska påståenden. De enkla räknelagarna
följer direkt från definitionen och är koordinatfria. Det är först under rubriken "beräkning av vektorprodukten" som man plötsligt kastar in ett koordinatsystem.
D4NIEL skrev:PATENTERAMERA skrev:Bokens härledning är dessutom lite fusk, eftersom man utnyttjar algebraiska egenskaper hos kryssprodukten som inte först bevisats gälla med utgångspunkt från bokens geometriska definition, detta är inte helt trivialt att göra.
Jag förstår inte, vilka algebraiska egenskaper menar du? Definitionen innehåller bara två geometriska påståenden. De enkla räknelagarna
följer direkt från definitionen och är koordinatfria. Det är först under rubriken "beräkning av vektorprodukten" som man plötsligt kastar in ett koordinatsystem.
rfloren använder koordinatformeln för att visa att a x b = -(b x a). Men koordinatformeln är inte definitionen av kryssprodukten i mekanikboken.
Så man bör först bevisa koordinatformeln utifrån bokens definition om man med denna vill visa att kryssprodukten är antisymmetrisk.
Bokens bevis fuskar lite eftersom man utnyttjar att kryssprodukten är distributiv, något som inte först visas med utgångspunkt från definitionen, inte helt trivialt. Sedan utnyttjar man i beviset att kryssprodukten är antisymmetrisk, så om man vill använda koordinatformeln för att visa antisymmetri så kan man inte basera formeln på detta bevis, eftersom det utnyttjar det som man vill bevisa.
PATENTERAMERA skrev:
Bokens bevis fuskar lite eftersom man utnyttjar att kryssprodukten är distributiv,
Ja, då förstår jag vad du menar, men boken använder inte den distributiva lagen för att visa att , det följer direkt ur den geometriska definitionen. Fuskandet inträder först under rubriken "Beräkning av vektorprodukten"
Vill man göra en uppdelning av vektorprodukten i komposanter måste man förvisso utnyttja den distributiva lagen. Man kan bevisa den på ett elegant vis genom att först definiera den skalära trippelprodukten helt geometriskt.
Trådskaparen hade problem med att förstå varför a x b = -(b x a). rfloren påpekade att man kunde bevisa det med komponentformeln, vilket är korrekt om man utgår från denna som definition. Jag ville bara visa på att om man vill använda komponentformeln för att visa antisymmetrin så får man inte först använda antisymmetrin när man härleder komponentformeln.
rfloren skrev:destiny99 skrev:Pieter Kuiper skrev:PATENTERAMERA skrev:måste du lära dig någon form av högerhandsregeln för kryssprodukten
Det brukar räcka med att veta att Och determinantformeln.
Varför är det ett minustecken framför b och varför är det lika med b×a? Är det omvänd kryssprodukten?
Beviset för att a x b = -b x a vid vektorprodukt är baserat på definitionen av vektorprodukten. Anta att vi har vektorerna a = [a1, a2, a3] och b = [b1, b2, b3]. Vektorprodukten av a och b, a x b, är definierad som [a2 * b3 - a3 * b2, a3 * b1 - a1 * b3, a1 * b2 - a2 * b1] (se boken)
Om vi nu beräknar b x a, vi får [b2 * a3 - b3 * a2, b3 * a1 - b1 * a3, b1 * a2 - b2 * a1]. Som du kan se, detta är exakt det negativa av a x b, och så a x b = -b x a.
Jag har lite svårt att förstå beviset dels hur kryssprodukten ger oss a×b och dels det negativa av axb.




