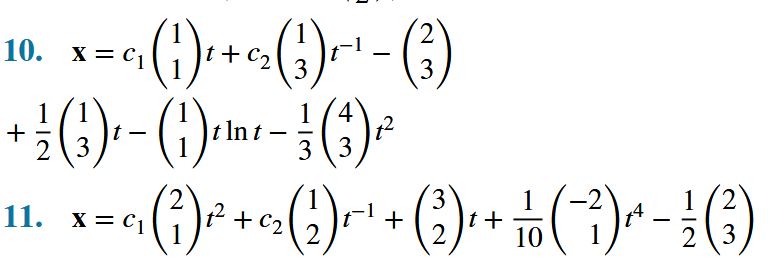Verify that the given vector is the general solution of the corresponding homogenous system

Vet inte vilken upplaga på Boyce m.fl. du har, men i 11:e upplagan lyder uppgifter 10-11 så här:

Här är det alltså $\mathbf{x}^{(c)}$ som man får kontrollera att den uppfyller diff:ekvationen.

LuMa07 skrev:

Vet inte vilken upplaga på Boyce m.fl. du har, men i 11:e upplagan lyder uppgifter 10-11 så här:

Här är det alltså $\mathbf{x}^{(c)}$ som man får kontrollera att den uppfyller diff:ekvationen.

Hejsan! Skönt att du kommenterat nu. Jag har upplaga 12. Mina frågor är de jag postat i #1. Ojdå det verkar som att de har inte gett oss  x^(c). Men ska absolut kontrollera mha din bild. Tack!

Bra! Här är facit från 11:e upplagan:

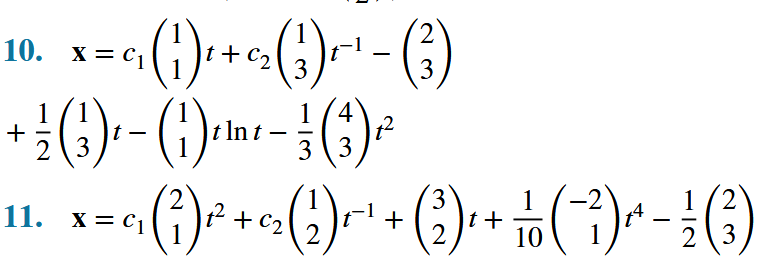
LuMa07 skrev:

Bra! Här är facit från 11:e upplagan:

Tack. Men hur är det tänkt att man ska lösa non homogenous system i uppgift 11? 

Man kan använda sig av metoden som boken kallar för "Variation of Parameters".

När man ska hitta en partikulär lösning till det inhomogena systemet

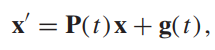
där man tagit fram den fundamentala matrisen $\mathbf{\Psi}(t)$ till det tillhörande homogena systemet, så söker man lösning på formen

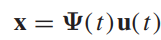
När detta sätts in i det inhomogena ekvationssystemet, så kommer man efter förenklingen få att

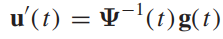
Vektorn $\mathbf{u}(t)$ hittar man genom att integrera detta och sedan sätts in det funna $\mathbf{u}$:t i sambandet $\mathbf{x}=\mathbf{\Psi}(t) \mathbf{u}(t)$.

I båda uppgifterna behöver man först dividera ekvationen med $t$, så att den blir skriven på formen x' = P(t)x + g(t). I uppgift 10 är alltså  $g\left(t\right) = \begin{pmatrix} 1/t -t \\ 2\end{pmatrix}$. Fundamentala matrisen är då $\Psi\left(t\right) = \begin{pmatrix} t & t^{-1} \\ t & 3t^{-1}\end{pmatrix}$. Använd dessa i formlerna ovan, ta fram u'(t), därefter u(t), och därefter x(t).

Varför den besynnerliga typografin i uppgiften? Betyder den något?

Trinity2 skrev:

Varför den besynnerliga typografin i uppgiften? Betyder den något?

I boken av Boyce–DiPrima–Meade har man följande typografiska regler:

• fetstilta raka gemener betecknar vektorer (och vektorvärda funktioner)
• fetstilta raka versaler betecknar matriser (och matrisvärda funktioner)

Författarna är någorlunda konsekventa när det gäller linjära differentialekvationer av första ordningen med att koefficienten vid oderiverade funktionen kallas för p(t), medan inhomogena delen kallas för g(t).

Det vete fåglarna varför det står hakparenteser med stora mellanrum kring matrisen i uppgift 10 medan runda parenteser kring matrisen i uppgift 11 i bokens 12:e upplaga. Man verkar ha infört nya typografiska brister i den senaste upplagan.