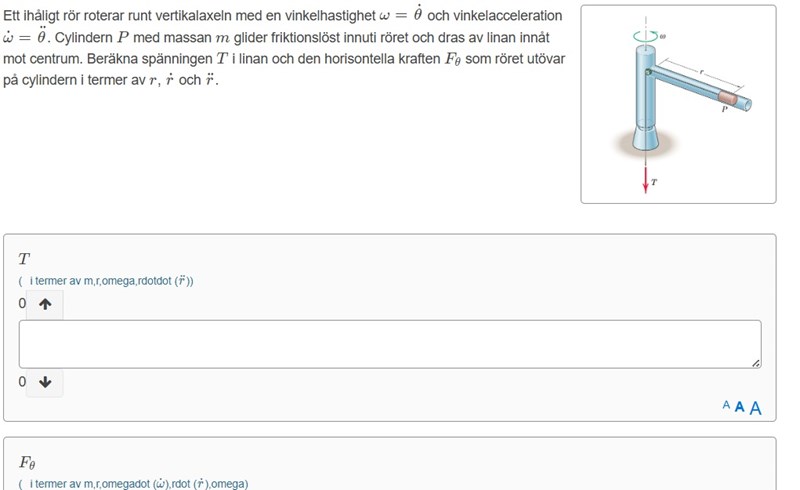
Vilka förkunskaper behövs innan jag börjar på denna? (Fysik/Universitet)

Acceleration i cylinderkoordinater.

$a_{r} = (\ddot{r} - r {\dot{θ}}^{2}) = F_{r} / m = T / m$

$a_{θ} = . . .$

PATENTERAMERA skrev:
Acceleration i cylinderkoordinater.

$a_{r} = (\ddot{r} - r {\dot{θ}}^{2}) = F_{r} / m = T / m$

$a_{θ} = . . .$

Men det med ihålighet och omega?

Vad?

PATENTERAMERA skrev:
Vad?

nvm ska kolla på det lmao. Det är bara att jag har sett flera uppgifter där det är något ihåligt men det kanske bara är till för att massan ska kunna glida i det

Ja massan glider i röret.

PATENTERAMERA skrev:
Ja massan glider i röret.

Nämen asså vad heter området mer. Liksom är typ uppgiften "ihåligt rör med glidande massa" för i plattformen vi gör uppgifterna står det inte vad det är för område som berörs.

Edit: du kanske inte vill höra det men ber om ursäkt för en "dum/tydlig" fråga. Ska vara helt ärlig, ibland kollar jag inte ens på uppgifterna innan jag postar och det kanske du märkt (eller inte) så ska bättra mig där.

Kolla upp om polära- eller cylinderkoordinater och hur hastighet och acceleration uttrycks i sådana koordinater. Då blir uppgiften lätt.

Från David Tongs föreläsningar som du kan ladda ner gratis från hans hemsida på Cambridges universitet.

PATENTERAMERA skrev:
Från David Tongs föreläsningar som du kan ladda ner gratis från hans hemsida på Cambridges universitet.

Du är så hjälpsam! Men vem är han, är det typ någon jag ska känna till lmao?

PATENTERAMERA skrev:
Från David Tongs föreläsningar som du kan ladda ner gratis från hans hemsida på Cambridges universitet.

Jaha vänta men detta känner jag till! Tack för en till källa i alla fall men jag har också en fråga:

Kan du förklara hur/varför enhetsvektorerna är skrivna som de är där han skriver "Written in Cartesian form, these vectors are..." och så skriver han dem på matrisform.

Edit: du hjälpte mig förstå var accelerationen kommer ifrån. Dock ett problem, det känns så konstigt ibland. T.ex. derivera x² så får man $2 x \hat{x}$ , du vet vanligtvis får man ju bara 2x du vet från gymnasiematten så det känns inte lika intuitivt. Här känner jag lite samma för sista termen i accelerationen då han "bara" lägger till $\dot{θ}$ i slutet. Idk det känns konstigt bara

Om man skulle vara noga skulle man tex skriva

$\vec{r} = r (\cos θ \hat{i} + \sin θ \hat{j})$ .

Om basvektorerna är underförstådda så brukar man bara skriva ut koordinaterna för vektorn in en radvektor eller en kolonnvektor. Dvs man skriver

$\vec{r} = r (\cos θ, \sin θ) = \{a l t .\} = r [\begin{matrix} \cos θ \\ \sin θ \end{matrix}]$ .

Vet inte hur du får derivatan av x² till 2x $\hat{x}$ .

Däremot så gäller det att $\nabla x^{2} = 2 x \hat{x}$ . Kanske är det det du tänkte på.

PATENTERAMERA skrev:
Vet inte hur du får derivatan av x² till 2x $\hat{x}$ .

Däremot så gäller det att $\nabla x^{2} = 2 x \hat{x}$ . Kanske är det det du tänkte på.

Å gudars uppgiften var inte så dålig. Nej men jag insåg nu varför $\dot{θ}$ , multipliceras i slutet. Det händer när man deriverar en bas enhetsvektor och m.a.p på vinkeln men eftersom vinkeln är m.a.p tid så används kedjeregeln.

Dock jag stötte på ett problem igen för när jag skulle få fram kraften T och det blev tecken fel. INGENSTANS i uppgiften står det vilket håll som är positivt eller negativt. Asså ja den dras inåt men hur vet man att inåt är negativt. Man kanske kan tänka sig att radien blir mindre men so what, tänk om det var positiv riktning? Så jag gissade på tecknet.

Edit: Är det delta upp och ner/gradient tecknet? Sen anledningen till varför jag inte förstod det sättet att skriva radien på är eftersom jag alltid ser sin = mot/hyp och cos = när/hyp (vilket ju stämmer) och i sådana falla så hade det blivit sin * j = j*mot/hyp alltså basically (mot*mot)/hyp och vice versa för cos fast med i. Men sen så måste man komma ihåg att det är en sorts projektion precis som i förra uppgiften så sin * j = j*mot bara för basvektorn "tar bort" alla andra basvektorer då de blir 0. Återigen, tack så mycket för förklaringen!

Jämför din friläggning med bilden av de polära koordinaterna (cylinderkoordinater):

Ser du åt vilket håll basvektorerna $\hat{r}$ och $\hat{\theta}$ pekar?

Åt det håll en basvektor pekar växer koordinaten. Så i bilden ovan växer r åt höger och $\theta$ uppåt.

Det gör att T pekar åt negativt $\hat{r}$ -håll. När du ställer upp Newton II i $\hat{r}$ -led Ska du alltså införa T med negativt tecken

$-T=m\left(\ddot{r}-r\dot{\theta}^2\right)$

När man frilägger (som du gjort ovan) är det en bra vana att alltid märka ut det koordinatsystem man tänkt använda så man vet åt vilket håll koordinaterna växer (är positiva).

D4NIEL skrev:
Jämför din friläggning med bilden av de polära koordinaterna (cylinderkoordinater):

Ser du åt vilket håll basvektorerna $\hat{r}$ och $\hat{\theta}$ pekar?

Åt det håll en basvektor pekar växer koordinaten. Så i bilden ovan växer r åt höger och $\theta$ uppåt.

Det gör att T pekar åt negativt $\hat{r}$ -håll. När du ställer upp Newton II i $\hat{r}$ -led Ska du alltså införa T med negativt tecken

$-T=m\left(\ddot{r}-r\dot{\theta}^2\right)$

När man frilägger (som du gjort ovan) är det en bra vana att alltid märka ut det koordinatsystem man tänkt använda så man vet åt vilket håll koordinaterna växer (är positiva).

Ahh, det make:ar sense. Tack så mycket!