Vilken är den 'optimala' presentationen av ett koordinatsystem?

Vi känner alla till:

och det används flitigt i svenska läroböcker.

Ser vi till "maskiner och hjälpmedel" finner man sälla dessa (utan besvärliga inställningar).

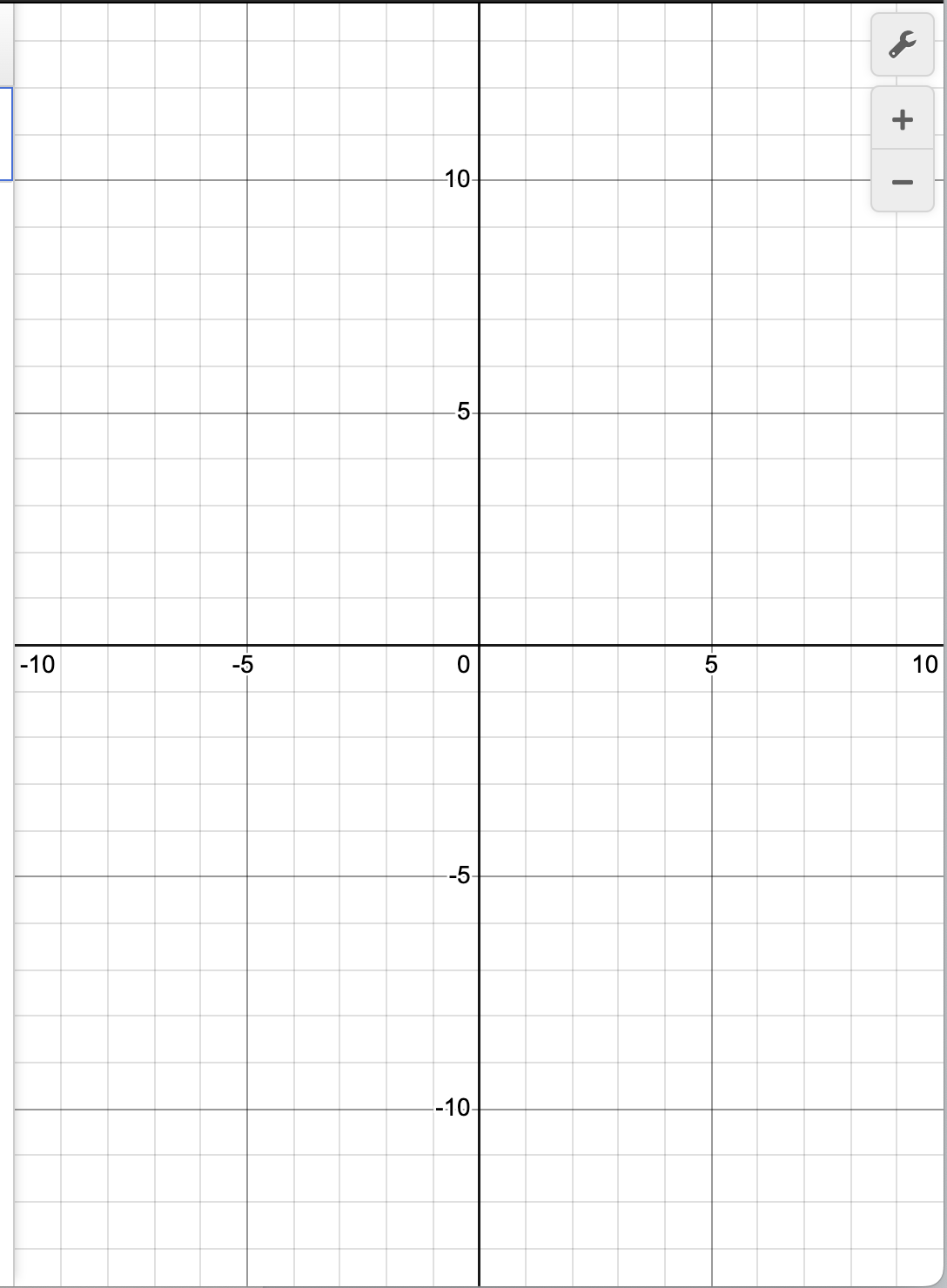
Desmos visar som standard

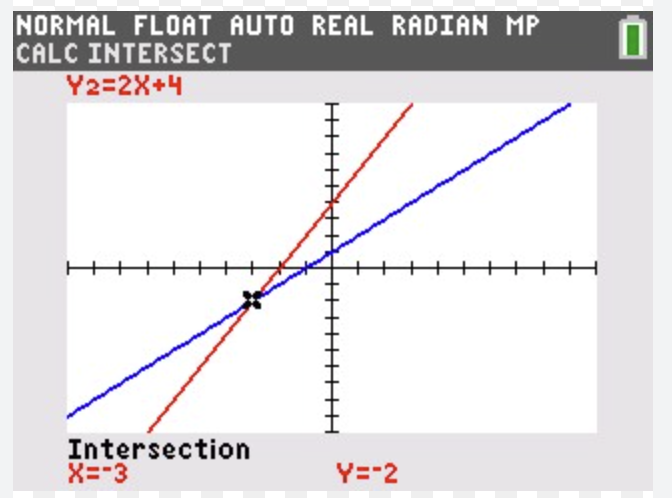
TI-84

Mathematica

PGF-plot

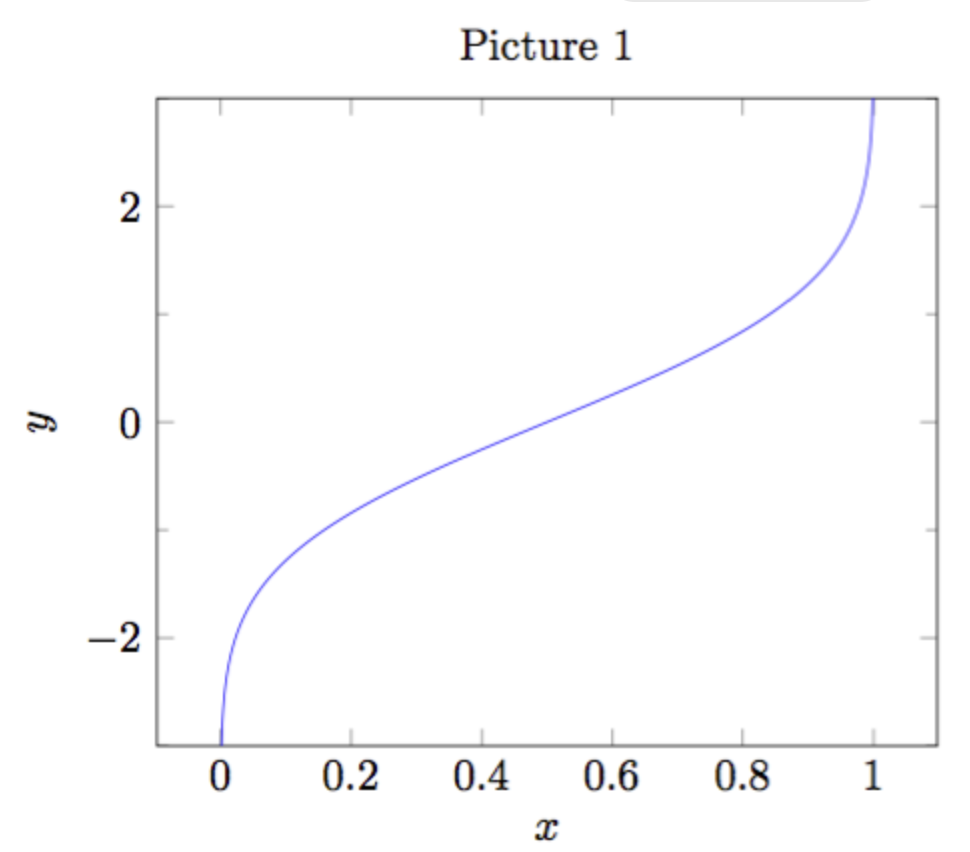
De 2 sista kan konfigureras i evighet, men vi fokuserar på "grundinställningen" tillsv.

MatLab har troligen något liknande;

Notera att ingen av dessa senare har pilar. Vissa har en ram runt grafen, eller kan lätt fås till det;

Ett par saker att observera

Pilar:

Behövs de? Fyller de någon funktion 2025? Har det någonsin förekommit pilar i en statistikgraf där t.ex. x-axeln är årtal? Vad händer om man vill presentera ett område som inte har axlarna "nära till hands"?

Det är klart att pilar har en poäng om man börjar betrakta vektorer m.m. men om "fokuset" i grafen ej innehåller axlarna spelarna några ev. pilarna ingen roll ändå, t.ex.

Notera att pilar kan läggas till i Desmos, vilket ger en 'underlig' representation av axlarna

Klara slut på grafen:

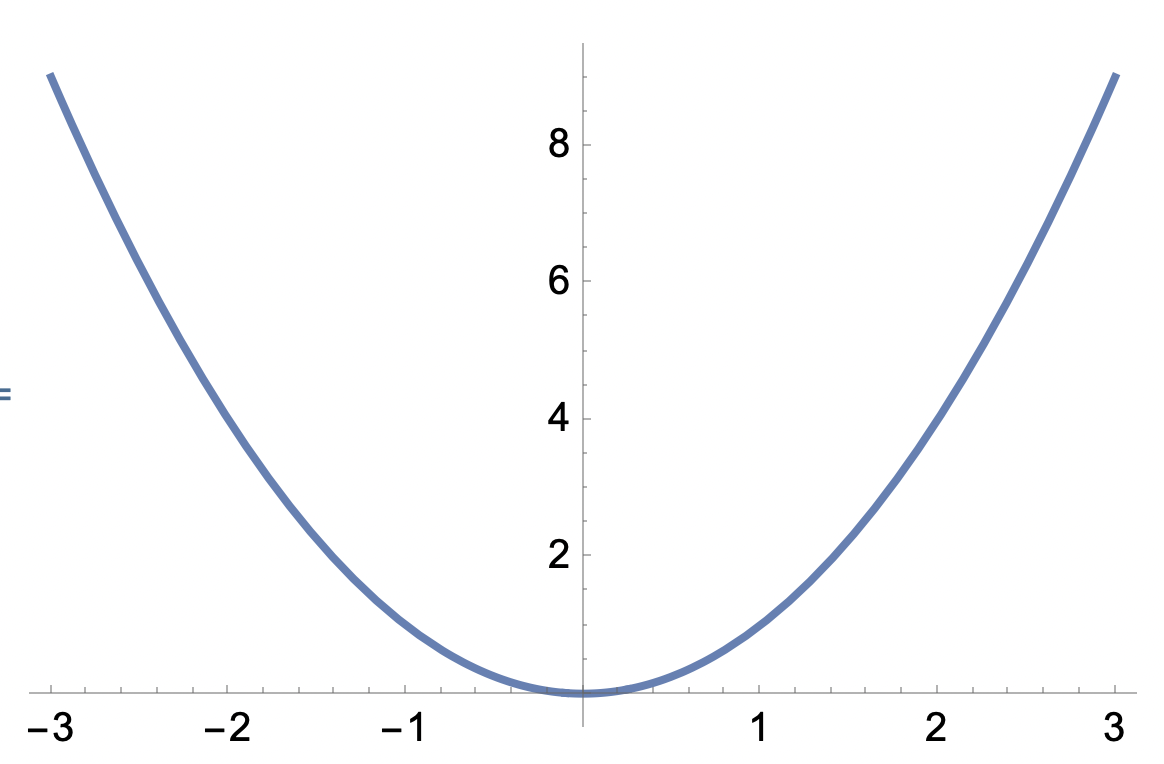
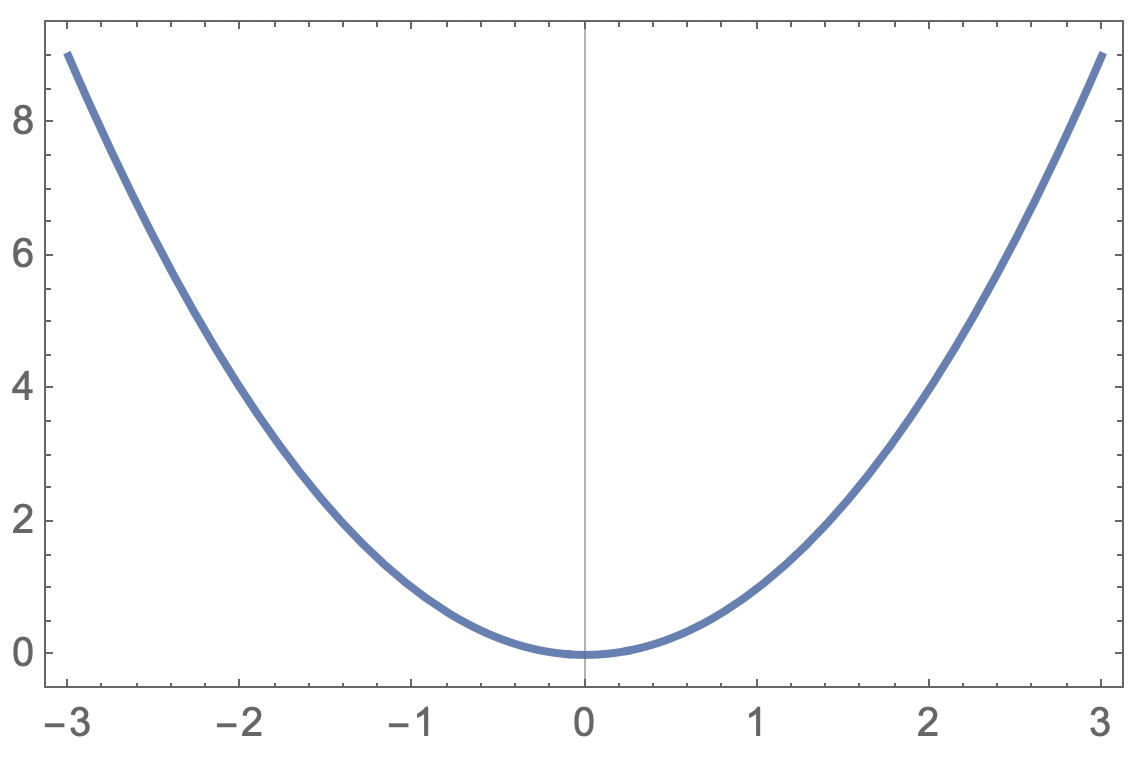
Tar grafen egentligen slut där bilden visar? Exempel

Detta är y=x^2 på -3≤x≤3 så ur den synpunkten har Mathematica ritat rätt, även om den utlämnat runda "prickar" i ytterkanterna enligt svensk skolstandard. Samma graf skulle kunna representera -3<x<3 utan något förtydligande från programmet. Många grafer i svenska läroböcker låter grafen sluta "när koordinatsystemet inte räcker till" och man frågar sig då vad är definition- och värdemängd. När jag ritade grafer (för hand) fortsatte jag alltid "svansarna" med streckade linjer för att visa att "det tar inte slut bara för att grafen tar slut". Det är ofta mkt. omständigt i de flesta ritprogram att få till. Troligen omöjligt på grafräknare. Streckade svansar var mycket förekommande under tidigt 1900-tal och man finner det i dåtidens böcker som säkert illustrerades av personer med bakgrund inom teknisk ritning.

Avsaknaden av "fyllda och tomma prickar" à la svensk skola skulle iofs kunna motivera/representera streckad linje, dv.s. "inga prickar" = "grafen fortsätter för evigt".

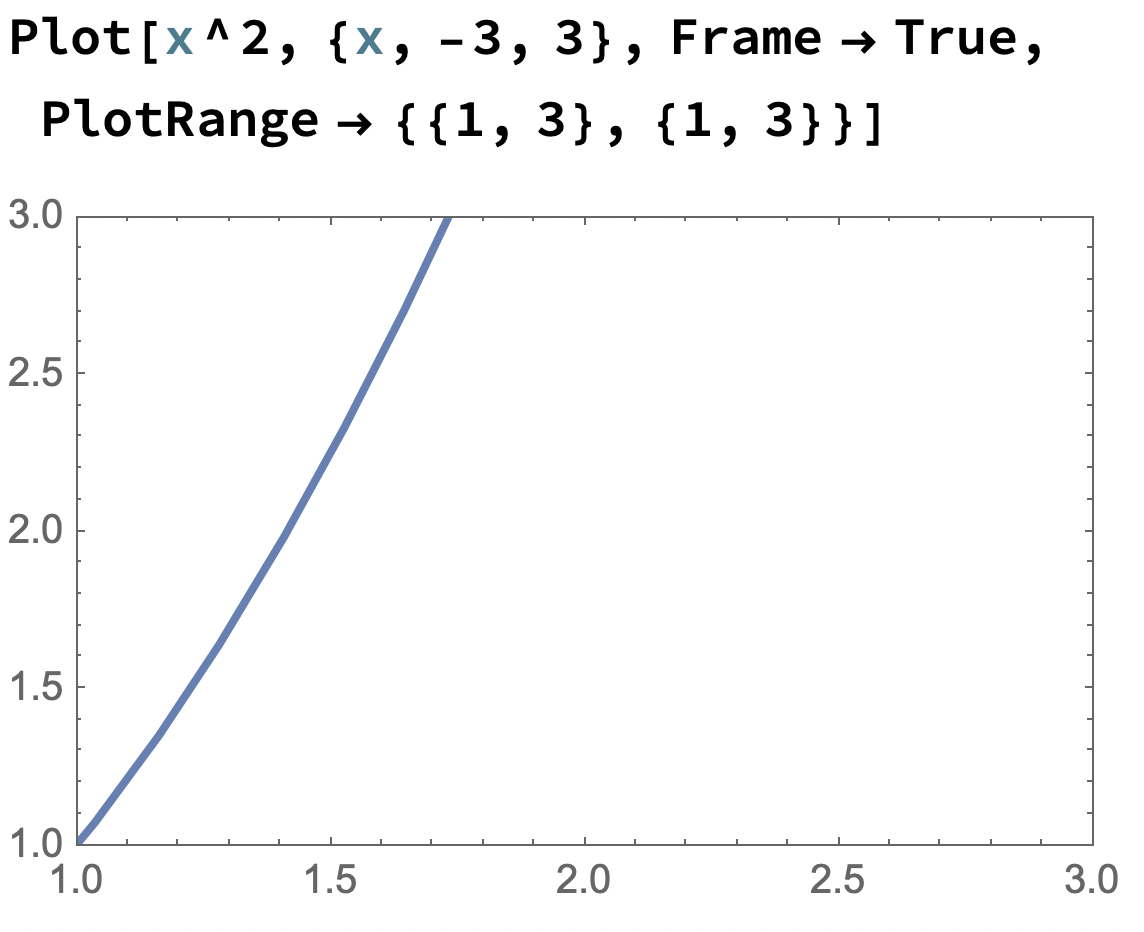
Man kan få Mathematica till att utelämna "tveksamma vita områden";

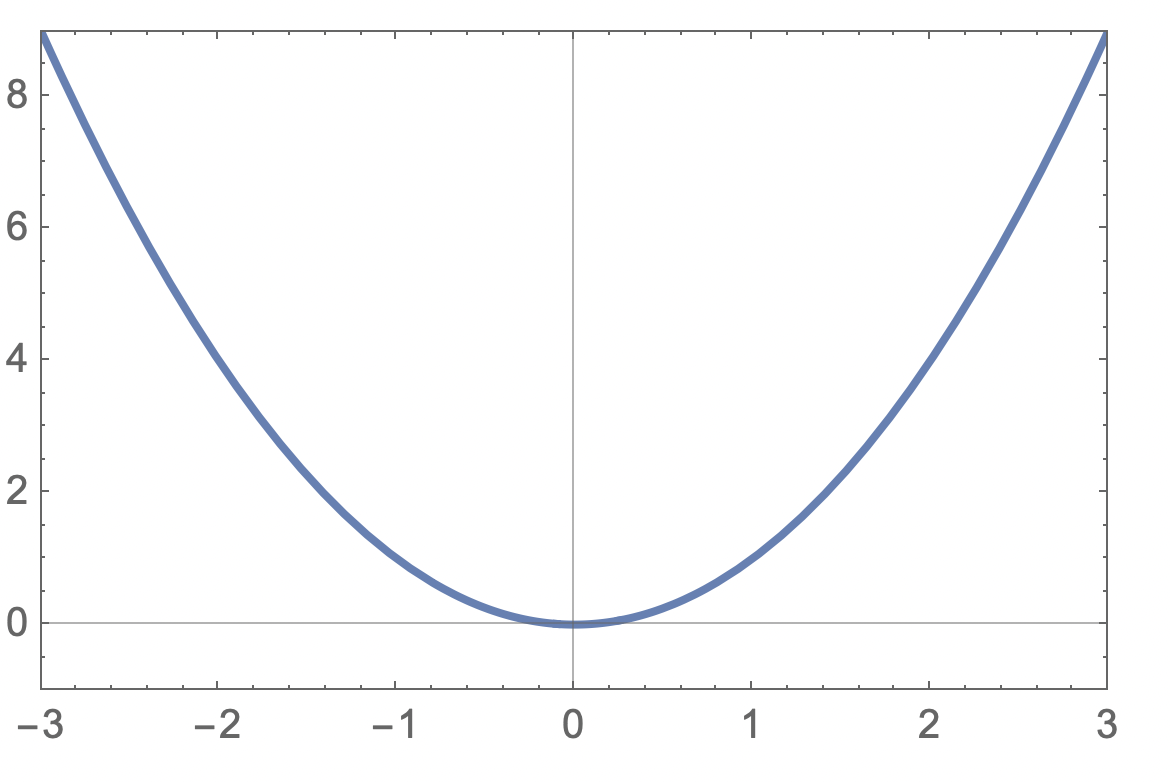
men vi har ej ännu tydligt visat funktionens definitions- och värdemängd.

Rutnät

En del läroböcker har har anammat ett rutnät som jag tror(!), utöver att det är lättare att läsa av värden, innebär "rityta", d.v.s. "vi ritar bara grafen på given rityta och ansvarar ej för vad som händer utanför". Detta är lite i Desmos tänk.

Nästa steg är att lägga på en ram och på så sätt ännu mera(?) isolera presenterad graf till ett "titthål". Det är den inlevelsen man t.ex. får av TI-84 där man betraktar en mycket större graf genom ett "titthål" (som man kan flytta runt).

En ram ger även möjlighet till dubbla skalor

vilket ett traditionellt koordinatsystem inte gör. Denna typ av graf är mycket snarlik de grafer som t.ex. Excel presenterar för statistik och datamängder.

Så vad är den optimala presentationen av ett koordinatsystemet enligt din mening? Det vore intressant att höra dina synpunkter, från alla nivåer inom matematik.