Vilken diameter har hålet om den första mörka ringen har diametern 20.5 cm på skärmen?
Hej!
Såhär löste jag uppgiften,men fick dessvärre felaktigt svar då rätt svar är 14 um. Vilken geometri ska man använda ? Min tanke är att det bildas en rätvinklig triangel där man kan få ut vinkel och därifrån kunna få fram diametern mha diffraktion från cirkulär yta.
Diffraktionsvinkeln är radie delad med avståndet till skärmen.
Det är alltid bra att göra en ritning.
Pieter Kuiper skrev:Diffraktionsvinkeln är radie delad med avståndet till skärmen.
Det är alltid bra att göra en ritning.
Okej jag var osäker på vilken ritning denna figur skulle ha eller hur den ska se ut. Vilken geometri utgår du ifrån när du säger " Diffraktionsvinkeln är radie delad med avståndet till skärmen. "? Jag tror jag tänkte något sånt också men vet ej varför det inte stämmer.
destiny99 skrev:
Rita den triangeln.
Pieter Kuiper skrev:destiny99 skrev:
Rita den triangeln.
Såhär tänkte jag mig. Då fick jag vinkeln 5.85.. grader
Och hur ligger då den mörka ringen?
Pieter Kuiper skrev:Och hur ligger då den mörka ringen?
Den hade ju en diameter på 20.5 cm.
Var i din figur ligger den ljusa fläcken i den mörka ringens mitt ?
Pieter Kuiper skrev:Var i din figur ligger den ljusa fläcken i den mörka ringens mitt ?
Jag tänkte sidan där det står 20.5 cm där ena prick till andra prick är mörka ringar. Jag vet inte hur det är man menar att det ska se ut i denna fråga. Men denna skiss är hur jag tänkte mig.
En Airy-skiva:
Pieter Kuiper skrev:En Airy-skiva:
Okej men var är geometrin här som beskrivs i uppgiften? Jag förstår att det är mörk ring som vi inte ser. Sen vet jag inte vad saken bredvid är där med olika decimaltal?
Alltså, ringens diameter är inte samma sak som ringens radie.
Den innersta mörka ringen har en radie på 1,22 lambda/d . Dess diameter är given som 20,5 cm.
Pieter Kuiper skrev:Alltså, ringens diameter är inte samma sak som ringens radie.
Den innersta mörka ringen har en radie på 1,22 lambda/d . Dess diameter är given som 20,5 cm.
Jag förstår tyvärr inte vad du menar när det saknas en figur också. Jag är med på all information som ges i frågan,bara att jag inte vet hur de vill att geometri ska se ut med den där ringen. Sen vet jag inte vad som är fel med min figur i #5.
Då får någon annan försöka förklara.
destiny99 skrev:Pieter Kuiper skrev:Alltså, ringens diameter är inte samma sak som ringens radie.
Den innersta mörka ringen har en radie på 1,22 lambda/d . Dess diameter är given som 20,5 cm.
Jag förstår tyvärr inte vad du menar när det saknas en figur också. Jag är med på all information som ges i frågan,bara att jag inte vet hur de vill att geometri ska se ut med den där ringen. Sen vet jag inte vad som är fel med min figur i #5.
Texten ger tillräcklig med information för att kunna rita.
Figuren borde se ut typ så här:
Pieter Kuiper skrev:destiny99 skrev:Pieter Kuiper skrev:Alltså, ringens diameter är inte samma sak som ringens radie.
Den innersta mörka ringen har en radie på 1,22 lambda/d . Dess diameter är given som 20,5 cm.
Jag förstår tyvärr inte vad du menar när det saknas en figur också. Jag är med på all information som ges i frågan,bara att jag inte vet hur de vill att geometri ska se ut med den där ringen. Sen vet jag inte vad som är fel med min figur i #5.
Texten ger tillräcklig med information för att kunna rita.
Figuren borde se ut typ så här:
Så avståndet mellan mörka ringen och centralmaximum är 20.5 cm eller är det från ena mörka ring till den andra mörka ring som är 20.5 cm?
destiny99 skrev:Så avståndet mellan mörka ringen och centralmaximum är 20.5 cm eller är det från ena mörka ring till den andra mörka ring som är 20.5 cm?
Uppgiften säger att den första mörka ringen har diametern 20,5 cm.
Pieter Kuiper skrev:destiny99 skrev:Så avståndet mellan mörka ringen och centralmaximum är 20.5 cm eller är det från ena mörka ring till den andra mörka ring som är 20.5 cm?
Uppgiften säger att den första mörka ringen har diametern 20,5 cm.
Aa okej, men var i figuren är det ju sin(v)=r/L? Man kanske ska approximera att radien från mittpunkten på den första mörka ringen till centralmaxima
destiny99 skrev:Aa okej, men var i figuren är det ju sin(v)=r/L? Man kanske ska approximera att radien från mittpunkten på den första mörka ringen till centralmaxima
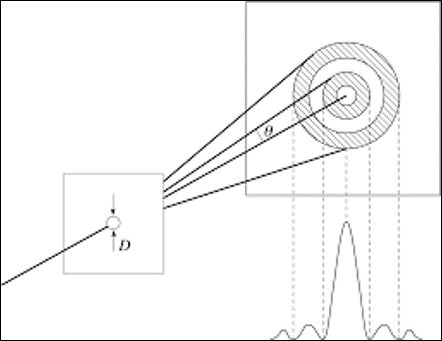
Pieter Kuiper skrev:destiny99 skrev:Aa okej, men var i figuren är det ju sin(v)=r/L? Man kanske ska approximera att radien från mittpunkten på den första mörka ringen till centralmaxima
Jag hittade också liknande bild på youtube. Nu förstår jag bättre varför det ska räknas ut som det gör. De tog också sinv=r/L
