Vilken energi verkar i de olika lägena? (Mekanik)

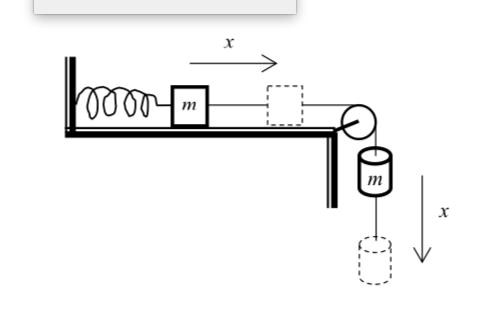
Om jag delar upp energin i två lägen enligt ovan bild så får jag i läge 1: vilket också är rätt. I läge 2 ska det vara vilket jag är med på, men varför ska inte lägesenergin tas med i beräkning i detta läge också? Även om vikten nått golvet så är ju lådan fortfarande på en höjd ovan marken (?) Jag har antagligen missuppfattat allt, men vänligen förklara då för mig för mig varför jag jag tänker fel.
massans (viktens) lägesenergi minskar mgx
Christopher skrev:massans (viktens) lägesenergi minskar mgx
Okej, menar du att vikten minskar lådans lägesenergi? Om så är fallet, varför?
Om du vill kan du räkna med lådans potentiella energi. I det första läget befinner sig både lådan och vikten på höjden x. Hastigheten för såväl låda som vikt är 0 precis när de släpps.
I vändläget är hastigheten återigen noll, men den här gången har vikten ingen potentiell energi. Däremot har lådan kvar sin energi. Lådan är ju på samma höjd som innan.
Det har också lagrats energi i fjädern.
Energin bevaras (ingen friktion), alltså måste
abcdefg skrev:Christopher skrev:massans (viktens) lägesenergi minskar mgx
Okej, menar du att vikten minskar lådans lägesenergi? Om så är fallet, varför?
Nej. Lådans lägesenergi är konstant. Den är på samma höjd.
Vikten minskar med mgx och fjädern ökar med 0.5kx2
Om lådan glider friktionsfritt är mgx = 0.5kx2
Vid vändläget är all rörelseenrgi = 0, precis som den var innan systemet släpptes.
Precis som Jroth har också föklarat.
Jroth skrev:Om du vill kan du räkna med lådans potentiella energi. I det första läget befinner sig både lådan och vikten på höjden x. Hastigheten för såväl låda som vikt är 0 precis när de släpps.
I vändläget är hastigheten återigen noll, men den här gången har vikten ingen potentiell energi. Däremot har lådan kvar sin energi. Lådan är ju på samma höjd som innan.
Det har också lagrats energi i fjädern.
Energin bevaras (ingen friktion), alltså måste
Tack! Nu blev det mycket tydligare.



