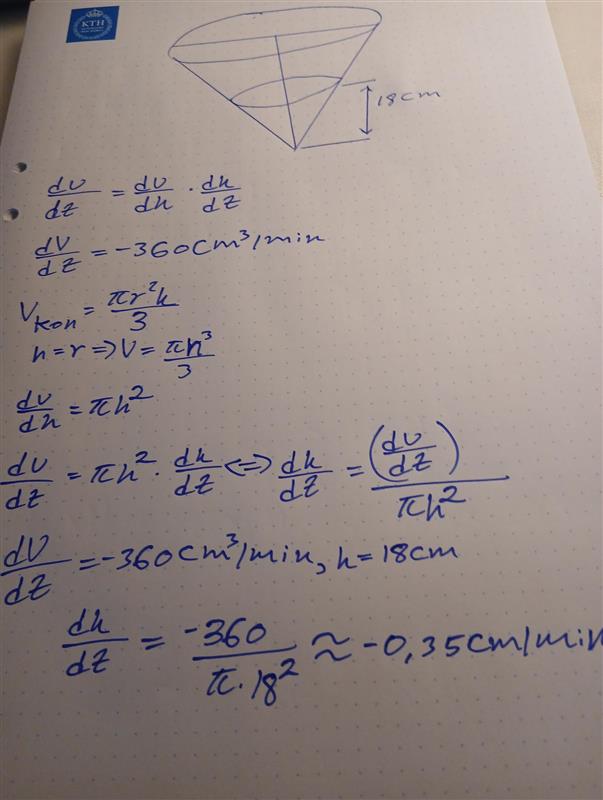Vilken hastighet ändras vätskenivån

Asså jag lite problem med att ställa upp sambanden.

Kan jag tänka mig V=$\frac{{\mathrm{\pi r}}^2}{3}$h

och ta dess derivata med avseende på r och h ?

Bra början.

Vad kan du säga om h jfrt r?

Trinity2 skrev:

Bra början.

Vad kan du säga om h jfrt r?

Är det hur jag deriverar med avseende på höjden jämfört med radien ?

Jag kan inte följa din tankegång men det ser ut som att det numeriska svaret är rätt.

De är omöjligt att säga om dina räkningar är fel då det inte framgår klart vad som händer. Det är inte troligt att en sådan räkning skulle ge fullt poäng. Kanske det finns någon aktiv lärare på PA som kan bedöma det bättre.

Trinity2 skrev:

Jag kan inte följa din tankegång men det ser ut som att det numeriska svaret är rätt.

De är omöjligt att säga om dina räkningar är fel då det inte framgår klart vad som händer. Det är inte troligt att en sådan räkning skulle ge fullt poäng. Kanske det finns någon aktiv lärare på PA som kan bedöma det bättre.

Har du möjlighet att visa en "tjusigare" lösning ?

Svarar eftersom Trinity2 är offline.

"Tjusigare" vet jag inte, men jag skulle göra så här:

Kedjeregeln ger oss $\frac{dV}{dt}=\frac{dV}{dh}\cdot\frac{dh}{dt}$

Vi känner till $\frac{dV}{dt}=-360$ cm³/min och söker $\frac{dh}{dt}$

Vi behöver alltså bestämma $\frac{dV}{dh}$

Volymen av en kon är $V=\frac{\pi r^2h}{3}$

Eftersom det för denna kon gäller att $h=r$ överallt så får vi att $V=\frac{\pi h^3}{3}$, vilket ger oss att $\frac{dV}{dh}=\pi h^2$

Sätter vi ihop detta så får vi

$\frac{dV}{dt}=\pi h^2\cdot\frac{dh}{dt}$, dvs $\frac{dh}{dt}=\frac{\frac{dV}{dt}}{\pi h^2}$

Med $\frac{dV}{dt}=-360$ cm³/min och $h=18$ cm får vi

$\frac{dh}{dt}=\frac{-360}{\pi\cdot18^2}\approx-0,35$ cm/min.

Svar: Vätskenivån minskar med cirka 3,5 mm/min.

står $h$ för höjden eller för hastighet ?

Vanligtvis burkar hastighet betecknas med $v$ för "velocity"

Yngve skrev:

Svarar eftersom Trinity2 är offline.

"Tjusigare" vet jag inte, men jag skulle göra så här:

+1

Jag hade gjort på samma sätt (ungf.). 

Arup skrev:

står $h$ för höjden eller för hastighet ?

Vanligtvis burkar hastighet betecknas med $v$ för "velocity"

Förlåt, jag var otydlig.

Jag borde ha förklarat de obekanta storheterna: V är volymen i cm³, h är höjden i cm och r är radien i cm:

så var inte det efterfrågade värdet dv/dt ?

Eftersom i texten står det

Arup skrev:

så var inte det efterfrågade värdet dv/dt ?

Eftersom i texten står det

Nej, då hade det nog stått "förändras volymen". Nu är det nivån man är ute efter, alltså höjden.

Arup skrev:

så var inte det efterfrågade värdet dv/dt ?

... och dV/dt var ju redan given, nämligen -360 cm³/min.

jag tror anledningen till varför det här svårare att begripa är för att jag mer van att uttryck derivator så här:

$$\begin{gathered} v\text{'}\left(h\right) \\ v\text{'}\left(t\right) \\ v\text{'}\left(r\right) \end{gathered}$$

Arup skrev:

jag tror anledningen till varför det här svårare att begripa är för att jag mer van att uttryck derivator så här:

$$\begin{gathered} v\text{'}\left(h\right) \\ v\text{'}\left(t\right) \\ v\text{'}\left(r\right) \end{gathered}$$

Japp, jag förstår.

Men just när det gäller kedjeregeln och uttryck som "derivera med avseende på xxx" så är det en bra idé att lära sig det som kallas Leibniz notation, dvs att uttrycka derivator på formen $\frac{dV}{dt}$ o.s.v.

gjorde samma sak som yngve i #9