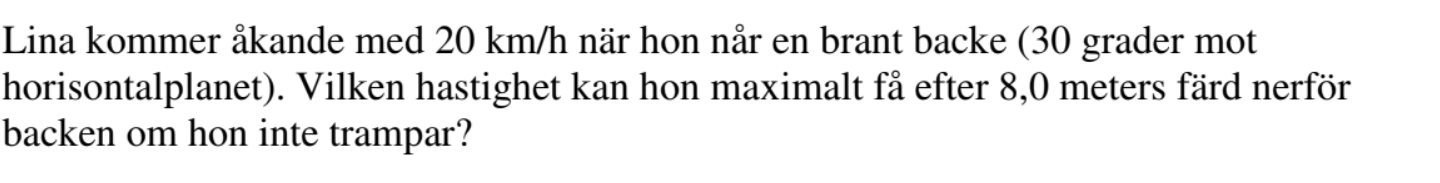Jag tänker mig det hör scenariot

Här är det bra att betrakta den mekaniska energins bevarande.
Rörelseenergi+lägesenergi är konstant
Ture skrev:Här är det bra att betrakta den mekaniska energins bevarande.
Rörelseenergi+lägesenergi är konstant
Jag jobbar inte med det. Jag ska utgå från det jag lärt mig tiigare dvs kraft+rörelse.
Ok, då får du använda de vanliga sambanden för hastighet tid och acceleratin.
En bra start är att beräkna accelerationen
Enligt Newtons 2:a lag gäller
är kraften samma sak som tyngdkraften i det här fallet ?
Ja, men du måste ta fram komposanten som verkar backena riktning
Ture skrev:Ja, men du måste ta fram komposanten som verkar backena riktning
Menar du så här ?

Den accelerande kraften är parallell med backen
Ture skrev:Den accelerande kraften är parallell med backen
Vad innebär det ?
du har delat upp tyngdkraften mg i två komposanter,
en vinkelrät mot marken: mg*cos(30)
och en parallell med marken: mg*sin(30)
Det är den som är parallell med marken som ger acceleration nerför backen, den andra ger upphov till en normalkraft på flickan.
ok, då ska jag använda mgsin(30)
jag har ingen massa. Hur gör jag då ?
Ture skrev:du har delat upp tyngdkraften mg i två komposanter,
en vinkelrät mot marken: mg*cos(30)
och en parallell med marken: mg*sin(30)
Det är den som är parallell med marken som ger acceleration nerför backen, den andra ger upphov till en normalkraft på flickan.
Har du nån till varför den ger upphov till accelerationen jag har svårt att koppla det
Vi har kraftekvationen
F = a*m
nu vet vi att F = mg*sin(30), då sätter vi in det:
mg*sin(30) =a*m
som du kan förenkla och lösa ut a
Jag har en fråga eftersom
Skulle inte vi då kunna ställa upp ekvationen:
Arup skrev:Jag har en fråga eftersom
Skulle inte vi då kunna ställa upp ekvationen:
Nej,
mgsin(30) är kraften, alltså
mgsin(30) = F = ma
Om du delar alla led med m får du
g*sin(30) = F/m = a
eftersom sin(30) = 0,5 har vi alltså
a = 0,5g
Jag får det till 4,91 m/s^2.
Jag undrar vad är mg*cos(30) och det här fallet ?
Arup skrev:Jag får det till 4,91 m/s^2.
Ja det är accelerationen. Vad frågade man efter?
Jag undrar vad är mg*cos(30) och det här fallet ?
Det är kraften mot marken. Lika stor är normalkraften från marken.,
Man kan räkna på energier. Efter 8 meter längs backen har hon tappat lägesenergi för 4 meter fallhöjd, som ökar rörelseenergin med lika mycket, d v s mgx4 (Massorna går bort, rörelseenergierna är
mv2/2
"Maximalt" innebär noll friktion och luftmotstånd
Nu kan jag väl använda den tidlösa formeln för att få fram den maximala hastigheten?
Arup skrev:Nu kan jag väl använda den tidlösa formeln för att få fram den maximala hastigheten?
Det går bra!
jag undrar räknar jag hastigheten i x-led eller i y-led i det här fallet ?
Du räknar rörelsen utmed backen, 30 graders lutning mot horisontalplanet. Några x eller y riktningar har vi inte blandat in här.
Ture skrev:Du räknar rörelsen utmed backen, 30 graders lutning mot horisontalplanet. Några x eller y riktningar har vi inte blandat in här.
Borde jag göra det ?
Är det så här man löser uppgiften ?

I väntan på att du får lära dig att räkna på energins bevarande är det här en bra metod. Bra att du avrundade till 2 siffror.
Jag tycker du ska svara i km/h eftersom uppgiften var given i den enheten. Men det kanske är onödigt.
Ture skrev:I väntan på att du får lära dig att räkna på energins bevarande är det här en bra metod. Bra att du avrundade till 2 siffror.
Jag tycker du ska svara i km/h eftersom uppgiften var given i den enheten. Men det kanske är onödigt.
ok då multiplicerar jag svaret med 3,6 och får då: km/h.
Tillägg: 22 sep 2025 09:34
Skulle du kunna visa mig hur löser den mha rörelsemängdens bevarande. Jag är nyfiken på lösningen.
Räkna med många siffror, avrunda enbart på slutresultatet.
10,46*3,6 = 37,6 avrundas till 38 km/h
Med energibetraktelse
Begynnelseenergi = mv2/2 +mgh = m(20/3,6)2/2 +0
Energi på slutet, mvs2/2 + mgh = mvs2/2-mg*8*sin(30) (minus eftersom vi rört oss nedåt)
Sätt energierna lika
m(20/3,6)2/2 +0 = mvs2/2-mg*8*sin(30), förenkla
15,432 = vs2/2-4g =>
vs = m/s