Har jag tänkt rätt ?

Jag har gjort fel rätt svar ska vara 22kN
Vilka krafter verkar på hissen, alltså får den att accelerera i ena eller andra riktningen?
är det tyngdkraften och normalkraften ?
Ja, om du skall accelerera hissen med 5 ms-2 uppåt måste du först övervinna tyngdaccelerationen som verkar nedåt.
sictransit skrev:Ja, om du skall accelerera hissen med 5 ms-2 uppåt måste du först övervinna tyngdaccelerationen som verkar nedåt.
Jag förstår inte va du menar ?
Om du inte vill rita en hiss och rita ut alla krafter kan du börja så här: Om hissen bara hänger stilla, vilken kraft måste wiren klara då?
är det inga krafter
Arup skrev:är det inga krafter
Nej, i så fall kunde du ju hänga en hiss i en sytråd. Fundera lite mer. Eller rita lite.
Är det så här ?

sictransit skrev:Arup skrev:är det inga krafter
Nej, i så fall kunde du ju hänga en hiss i en sytråd. Fundera lite mer. Eller rita lite.
Jag har inte rikitigt koll känner jag. Men är svaret tyngdkraften ?
Det stämmer och du har räknat rätt. Någon normalkraft som du ritat har du dock inte om hissen hänger i en wire.
När hissen inte accelererar har du Fg (tyngdkraft) som drar hissen nedåt. Du har även F1w som är en spännkraft i wiren. Den är lika stor som Fg och motriktad. Summan av krafterna är noll.
När hissen accelererar uppåt tillkommer kraften F2w. Tillsammans med F1w är de större än Fg.
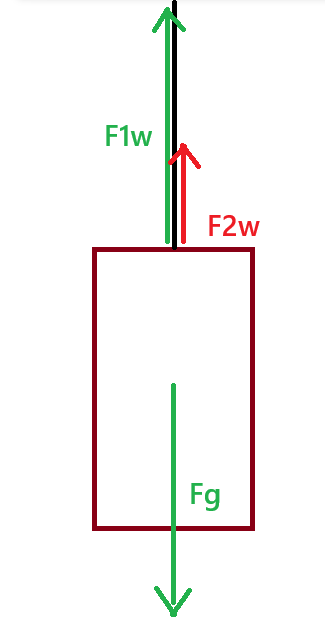
För att hissen ens skall börja accelerera uppåt måste du övervinna tyngdkraften, 1450*g, ca 14.2 kN.
Nu säger uppgiften att den skall accelerera 5 ms-2, vilket betyder ytterligare 1450*5 N, ca 7,3 kN.
Enklast är kanske att räkna på att wiren skall klara inte bara tyngdaccelerationen g utan även 5 ms-2, totalt ca 15 ms-2.


