Vilken rot har Mischa missat?
Hej! Jag löste på något mystiskt vis följande uppgift:
Under tiden jag gick igenom hennes lösning var min första tanke att den andra roten skulle vara 0. Det var rätt men den tanken var så snabb att jag inte hann med att förstå mitt resonemang innan jag glömde av det. Låter helt otroligt, men det är så! Nu försöker jag förstå hur roten i detta fall kan vara noll. Min gissning är att när hon gjorde så att alla x hamnade i samma led och differensen blev noll så betyder det att det som är i vänster led också ska vara lika med noll. Därför måste saker och ting multipliceras med noll.
för vilka ekvationer skulle detta isf gälla? Är det för alla ekvationer där noll är ensamt i ena ledet och variablerna är för sig i det andra, utan andra konstanter? Finns det någon gång en sådan potensekvation med svaret noll som saknar en reell lösning?
Läs på om nollprodukt och försök sen tänka ut varför 0 är en rot.
Antingen måste det inom parantesen vara lika med noll för att hela vänsterledet ska vara lika med noll, eller så måste det utanför parantesen vara lika med noll för att det ska stämma. 3^4=81 och 81-81=0 (-3)^4 = 81 återigen blir 81-81=0 Kvar blir (3^5)*0 =0 och likheten gäller. Om faktorn utanför parantesen skulle vara lika med noll, multipliceras allt innanför parantesen med noll och V.L blir 0. Likheten gäller.
Inte nog med det,
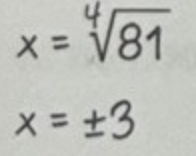
är fel. Det är som att säga rot(4)=±2
är det inte det då? vad jag har fått lära mig att det är så. 2^2=4 (-2)^2 =4
KlmJan skrev:är det inte det då? vad jag har fått lära mig att det är så. 2^2=4 (-2)^2 =4
Nej, skilj på en lösning till en ekv.
x^2=4 <=> x=±2
och operatorn "rot", rot(4)=2, inte –2.
aha, menar du "rot" som i svar på en ekvation?
KlmJan skrev:aha, menar du "rot" som i svar på en ekvation?
"rot" är bara en av många operatorer som kan användas i en ekvation. Vi måste skilja på lösningen till en ekvation och de grundläggande operatorn.
Tag t.ex. ekv.
2x=4
Här använder vi operatorn division och får x=4/2=2 och vi "framkallar" inte en negativ lösning bara för det. Det finns inga (vanliga) operatorer som framkallar "dubbelsvar". En operator ger "vanligtvis" endast ett svar. Testa på din räknar. Vad säger den om du skriver rot(4). Den kommer ej att ge -2. På samma sätt ger arctan(1)=π/4 (du kanske inte har kommit till trigonometri ännu så vi går inte djupare in på denna funktion).
Slutsats: En operator ger endast ett svar, det din miniräknare visar. En ekvation däremot kan ha flera svar, men det är INTE operatorn i sig som "framkallar" dem. Det finns andra bakomliggande anledningar till att ekvationen kan ha flera svar.
Oki, tack för förklaringen :)
