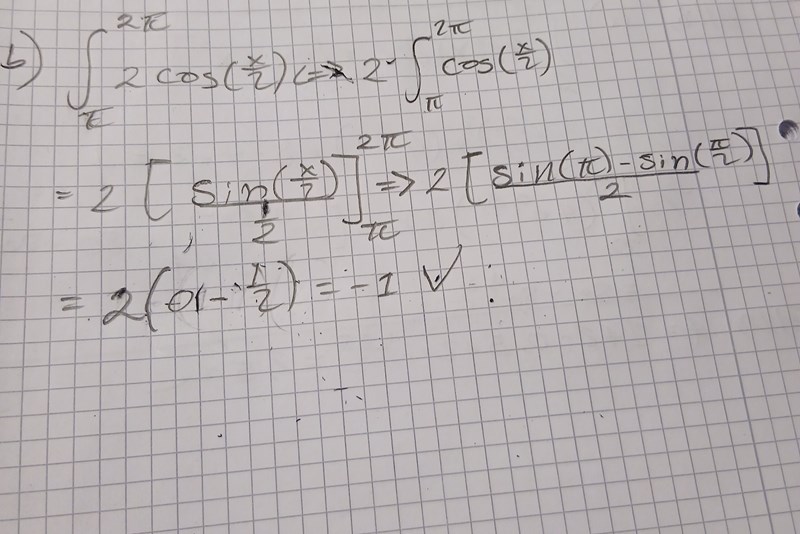Vilket fel gjordes ?

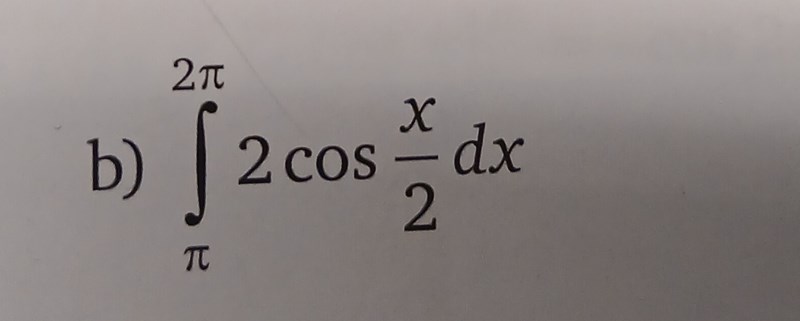
Tänk på att derivatan till $\sin\left(\frac x2\right)$ är $\frac 12 \cos\left( \frac x2\right)$

Så blir integralen$\frac{-\cos \left({\displaystyle \frac{x}{2}}\right)}{{\displaystyle \frac{1}{2}}}$ 

Nej din första primitiva funktion $\frac{\sin(x/2)}{1/2}$ var korrekt, men du bytte senare ut 1/2 mot 2 i nämnaren.

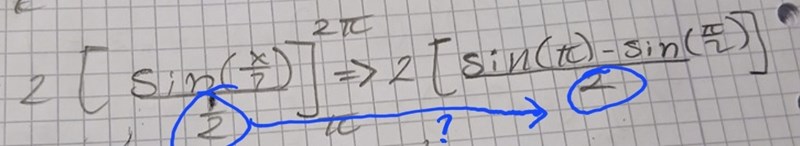
Ok så var det anledningen till att jag fick fel ?

Ja.

≈===

Ett bra tips när det gäller att lösa integraler är att alltid som första steg när man har tagit fram en primitiv funktion derivera denna och se om man då får tillbaka integranden.

Yngve skrev:

Nej din första primitiva funktion $\frac{\sin(x/2)}{1/2}$ var korrekt, men du bytte senare ut 1/2 mot 2 i nämnaren.

Ah, jag missade att det stod $1/2$ i den ursprungliga primitiven. Trodde det stod 2 i båda nämnare. 

Yngve skrev:

Ja.

≈===

Ett bra tips när det gäller att lösa integraler är att alltid som första steg när man har tagit fram en primitiv funktion derivera denna och se om man då får tillbaka integranden.

Det brukar jag göra när jag tar den primtiva funktionen av sinus resp. cos

Arup skrev:

Det brukar jag göra när jag tar den primtiva funktionen av sinus resp. cos

Bra, men du bör göra det alltid, oavsett hur integranden ser ut. Detta för att minska risken att räkna vidare på en felaktig lösning i onödan.

=======

Det är även ett bra sätt att snabbt hitta primitiva funktioner till icke-triviala funktioner.f(x)

1. Gissa en primitiv funktion F(x)
2. Derivera F(x)
3. Jämför F'(x) med f(x). Är de lika så är du klar, Om inte: Ta fram en ny gissning på F(x) och gå till steg 2.

Betonar att du ska derivera den primitiva funktionen som dyker upp, och inte det värde du får fram av den bestämda integralen i slutet. 

Mr. P jag förstår inte riktigt vad du menar ?

Du har inte gjort det felet, men det hade varit olyckligt om du råkat derivera talet som du får ut från en bestämd integral och alltid få 0 menar jag. 

Jag undrar varför blir den primitiva funktionen till $f\left(x\right)=\cos \left(\frac{x}{2}\right)$

$F\left(x\right)=-\sin \left(\frac{x}{2}\right)\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$

och inte$F\left(x\right)=-\sin \left(\frac{x}{2}\right)\hspace{0.17em}?$

Dwt är den inte. Den är 2*sin(x/2).

Eftersom F(x) är en sammansatt funktion så får du ut en faktor som är "den inre derivatan" när du deriverar den. I det här fallet är den 1/2.

Yngve skrev:

Dwt är den inte. Den är 2*sin(x/2).

Eftersom F(x) är en sammansatt funktion så får du ut en faktor som är "den inre derivatan" när du deriverar den. I det här fallet är den 1/2.

Kan man tänka på "keje regeln" ?

Dvs inre-yttre funktion 

Arup skrev:

Kan man tänka på "keje regeln" ?

Dvs inre-yttre funktion 

Ja, om ditt förslag på primitiv funktion är en sammamsatt funktion (som i det här fallet) så ska du som vanligt använda kedjeregeln vid derivering.

Men använd gärna metoden i svar #10 för att komma fram till rätt primitiv funktion.

Här är ett förslag på hur metoden kan tillämpas i detta fallet:

• f(x) = 2*cos(x/2)
• Jag gissar på en primitiv funktion F(x) = 2*sin(x/2)
• Jag deriverar min gissning (med hjälp av kedjeregeln): F'(x) = 2*cos(x/2)*(1/2) = cos(x/2)
• Jag jämför F'(x) med f(x) och ser att F'(x) är exakt hälften av vad den borde vara.
• Jag ändrar därför min gissning med en faktor 2. Ny gissning F(x) = 4*sin(x/2)
• Jag deriverar min nya gissning: F'(x) = 4*cos(x/2)*(1/2) = 2*cos(x/2)
• Jag jämför F'(x) med f(x) och ser att de är lika. Då är jag klar.

Resultat: F(x) = 4*sin(x/2) är en primitiv funktion till f(x) = 2*cos(x/2)