Vilket metod är bättre? fjäderberäkning

Hej

Jag gjorde en laboration där jag använde två metoder för att beräkna fjäderkonstanten. Den var att sätta olika vikter på en fjäder och när fjäder är i vila så gör jag ett diagram som liknar F=K*s där F=mg (kraftjämvikt). Jag fick att K=7.

Andra metoden var att hänga de olika vikterna (var för sig och samma vikter som i metod 1) på fjäder sedan låta fjädern svänga upp o ner med varje vikt. och med varje vikt beräknade jag tiden för 10 svängningar sedan tiden för en svängning i kvadrat för att därefter göra ett diagram $T^{2} = k m$ där lutning k skulle användas för att beräkna K genom $T = 2 π \sqrt{\frac{m}{k}}$ då

fick jag K=5. Nu min fråga vilken metod är bättre(mer noggran) att beräkna fjäderkonstanten med? kan det var den som hade en funktion som var mer lik rät linje när jag skapade ett diagram för varje metod?

Edit: det var lika många försök i både metoderna. 4 försök

Den metod som är mer exakt är den som har fler mätningar och färst felkällor. Du har angett för lite information för att någon ska kunna svara på din fråga.

Hur stort var m-värdet i de två linjära anpassningarna du gjorde?

Ebola skrev:
Den metod som är mer exakt är den som har fler mätningar och färst felkällor. Du har angett för lite information för att någon ska kunna svara på din fråga.
Hur stort var m-värdet i de två linjära anpassningarna du gjorde?

Det var samma antal försök i både metoderna (redigerade inlägget också). första metoden hade m=0.055 medan andra metoden hade m=0.048.

Okej, m-värdet är ibland en bra indikator men den är inte helt tillförlitlig då det i detta fall kan röra sig om systematiska fel och då spelar inte den någon roll då det är lutningen som söks.

Det som händer i andra metoden är att du egentligen får fler mätningar då du tar ett medelvärde på 10 svängningar vilket kan eliminera slumpmässiga fel i jämförelse med om du hade mätt tiden vid varje svängning.

För att nå samma noggrannhet i första mätningen måste du egentligen göra fler mätningar så att metoden med 10 svängningar är mer noggrann.

Kan du lägga upp dina mätdata?

Min första tanke var att de matematiska modellerna du använder kanske är olika bra att mäta k med. Har du någon fundering kring det?

Ebola skrev:
Okej, m-värdet är ibland en bra indikator men den är inte helt tillförlitlig då det i detta fall kan röra sig om systematiska fel och då spelar inte den någon roll då det är lutningen som söks.
Det som händer i andra metoden är att du egentligen får fler mätningar då du tar ett medelvärde på 10 svängningar vilket kan eliminera slumpmässiga fel i jämförelse med om du hade mätt tiden vid varje svängning.

För att nå samma noggrannhet i första mätningen måste du egentligen göra fler mätningar så att metoden med 10 svängningar är mer noggrann.
Kan du lägga upp dina mätdata?

Jaha, de sant jag hade missat det med antal försök. Här kommer mina mätdata:metod,1: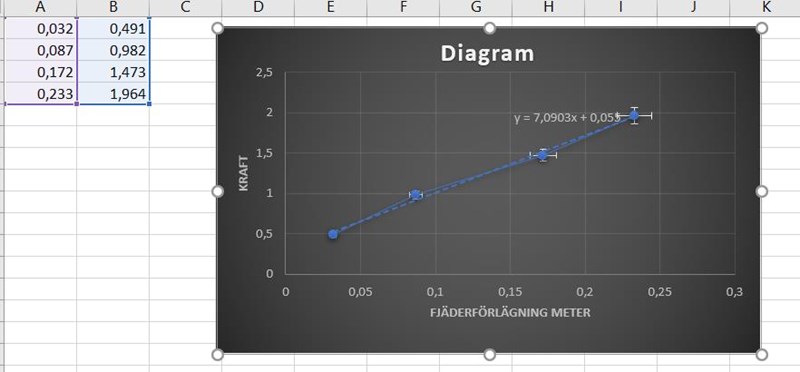

metod 2:

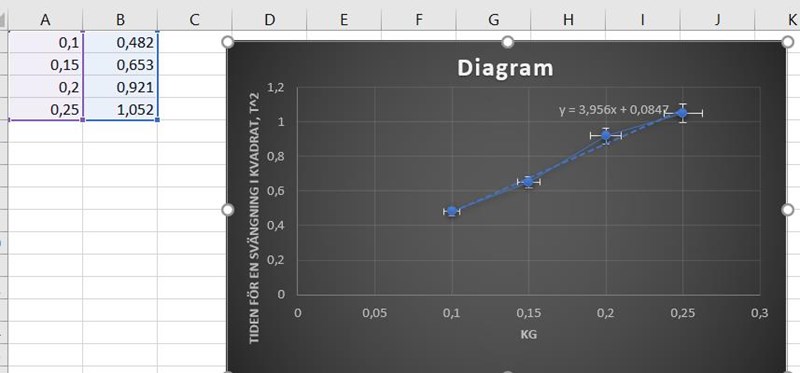
JohanF skrev:
Min första tanke var att de matematiska modellerna du använder kanske är olika bra att mäta k med. Har du någon fundering kring det?

jag förstår inte riktigt vad du menar med?

abbe59 skrev:
JohanF skrev:
Min första tanke var att de matematiska modellerna du använder kanske är olika bra att mäta k med. Har du någon fundering kring det?
jag förstår inte riktigt vad du menar med?

Metod1: Du gör en direkt mätning på själva definitionen av k. Enda felkällan är mätfel. (Längd och massa mäts statiskt, borde kunna bli hur noggrant som helst)

metod2: Indirekt mätning enligt och användande av matematisk modell som antas vara sann.
Är modellen sann i detta fall?

JohanF skrev:
abbe59 skrev:
JohanF skrev:
Min första tanke var att de matematiska modellerna du använder kanske är olika bra att mäta k med. Har du någon fundering kring det?
jag förstår inte riktigt vad du menar med?
Metod1: Du gör en direkt mätning på själva definitionen av k. Enda felkällan är mätfel. (Längd och massa mäts statiskt, borde kunna bli hur noggrant som helst)
metod2: Indirekt mätning enligt och användande av matematisk modell som antas vara sann.
Är modellen sann i detta fall?

När du skriver matematisk modell du menar 'formeln' eller hur? Och jag förstår inte riktigt hur skillnaden mellan direkt och odirekt kan påverka? det kanske finns fler värde i indirekt mätning vilket ger upphov till fler felkällor men som Ebola skrev så innehåller metod 2 fler försök, alltså bättre noggranhet.

Det är två helt olika typer av felkällor. En felkälla är mätfel. Den andra typen är modellfel.

Det jag menar är att modellfelet KANSKE är det dominerande felet. Det återstår att reda ut. Du kan prova att räkna baklänges för att se vilka mätvärden du skulle behöva vid respektive metod, för att få den andra metodens resultat. Kanske kommer du fram till att det skulle krävas helt orimliga mätfel (tex mäta fel på 10T med 2sekunder kortare än du verkligen gjorde, eller något annat jättekonstigt). Isåfall ska du nog försöka leta fel någon annanstans än i mätningarna.

Modellfel: Formeln för svängningstiden förutsätter att svängningen var odämpad harmonisk. Såg din svängning odämpad ut? Eller blev svängningen så liten att den stannade efter elva svängningar, typ? (hade du en helt odämpad svängning så har du uppfunnit evighetsmaskinen)

Såg svängningen harmonisk ut? Eller studsade fjädern kors och tvärs, och fjädern slog helt ihop ibland, typ?

Den typen av frågeställningar behöver man inte ens tänka på i metod1. Där kan man koncentrera sig på mätfel.

Som JohanF skriver är dina försök där du drar i fjädern en direkt mätning av fjäderkonstanten och det finns inga antaganden förutom att fjädern är elastisk. Detta antagande är att betrakta som en svag men viktig felkälla.

I andra experimentet har du inte bara ovan antagande om att fjädern är elastisk men även att fjädern svänger längs med en rät linje, att den följer en harmonisk rörelse och är odämpad. Alltså gör du fler antaganden när du applicerar modellen för $T=2\pi\sqrt{\dfrac{m}{k}}$ . Dessa antaganden är svårare att kontrollera än att bara hålla sig inom elastiska regionen när du drar ut en fjäder.

abbe59 skrev:

Hur fick du fjäderkonstanten 5 från detta?

$\displaystyle T^{2}=\dfrac{4\pi^{2}}{k}m$

Lutningen är alltså $\dfrac{4\pi^{2}}{k}$ .

Svara

Visa senaste svar