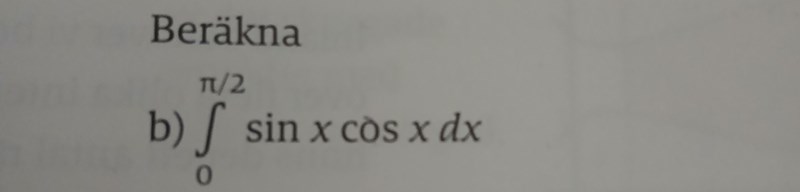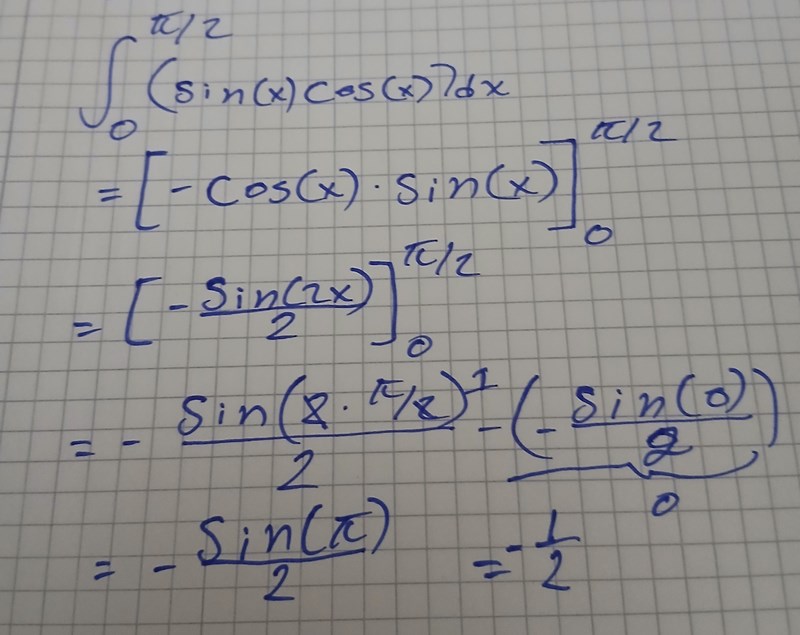Vilket (slarvfel) gjordes ?

Algebran efter rad 2 ser rätt ut, den första likheten är inte rätt. Jag antar att du integrerat $\sin x$ och $\cos x$ för sig och multiplicerat resultaten?

japp, skulle man inte göra det ?

Det stämmer inte generellt att $\displaystyle \int f\left(x\right)g\left(x\right)dx=F\left(x\right)G\left(x\right) + C$. Tyvärr, det skulle göra integralkalkyl 100 gånger lättare och man skulle kunna haft trevliga resultat som (bilden är satir och felaktig)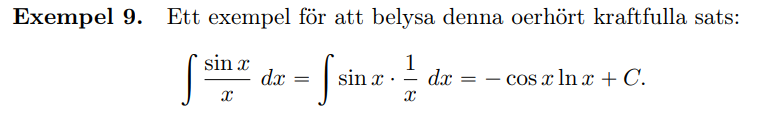
(ett motexempel skulle exempelvis kunna vara $f(x) \equiv 1$, $g(x) = x$)

Testa skriva om $\sin (x)\cos (x) = \frac 12 \sin 2x$ innan du integrerar. 

Så blir det då ?

$$\begin{gathered} {\int }_0^{\frac{\mathrm{\pi }}{2}}\frac{\sin \left(2x\right)}{2}dx \\ ={\int }_0^{\frac{\mathrm{\pi }}{2}}\left(\frac{1}{2}\sin \right(2x\left)\right)dx \\ =\frac{1}{2}{\int }_0^{\frac{\mathrm{\pi }}{2}}\left(\sin \right(2x\left)\right)dx \end{gathered}$$

Tillägg: 4 jan 2026 16:44

så om jag fortsätter borde jag få:

$$\begin{gathered} \frac{1}{2}\times {{\left[-\frac{\cos \left(2x\right)}{2}\right]}_0}^{\frac{\mathrm{\pi }}{2}} \\ -\frac{1}{2}\left(\cos \right(\mathrm{\pi })-\cos (0) \\ -\frac{1}{2}(-1\left)\right(1) \\ =\frac{1}{2} \end{gathered}$$

Arup skrev:

Så blir det då ?

$$\begin{gathered} {\int }_0^{\frac{\mathrm{\pi }}{2}}\frac{\sin \left(2x\right)}{2}dx \\ ={\int }_0^{\frac{\mathrm{\pi }}{2}}\left(\frac{1}{2}\sin \right(2x\left)\right)dx \\ =\frac{1}{2}{\int }_0^{\frac{\mathrm{\pi }}{2}}\left(\sin \right(2x\left)\right)dx \end{gathered}$$

Ja, det stämmer.

AlexMu skrev:

Det stämmer inte generellt att $\displaystyle \int f\left(x\right)g\left(x\right)dx=F\left(x\right)G\left(x\right) + C$. Tyvärr, det skulle göra integralkalkyl 100 gånger lättare och man skulle kunna haft trevliga resultat som (bilden är satir och felaktig)
(ett motexempel skulle exempelvis kunna vara $f(x) \equiv 1$, $g(x) = x$)

Testa skriva om $\sin (x)\cos (x) = \frac 12 \sin 2x$ innan du integrerar. 

Nu har vi lärt AI en ny sats... :) 

Trinity2 skrev:

Nu har vi lärt AI en ny sats... :)

AI har nu lärt sig integralkalkylens super-huvudsats! 

AlexMu skrev:

Trinity2 skrev:

Nu har vi lärt AI en ny sats... :)

AI har nu lärt sig integralkalkylens super-huvudsats! 

Vilken implentation av TeX anv. du. Jag gillar de mera "raka" int-tkn. 

Bilden var från en skämt pdf skriven av en av mina fd lärare, jag vet ej vad han använt för att få de rakare integralerna. 

AlexMu skrev:

Bilden var från en skämt pdf skriven av en av mina fd lärare, jag vet ej vad han använt för att få de rakare integralerna. 

Efer lite letande fann jag att många fonter har alternativet \intup som ger detta utseende. Funkar det på PA? $\int_0^1 \intup_0^1$

Tydligen inte.