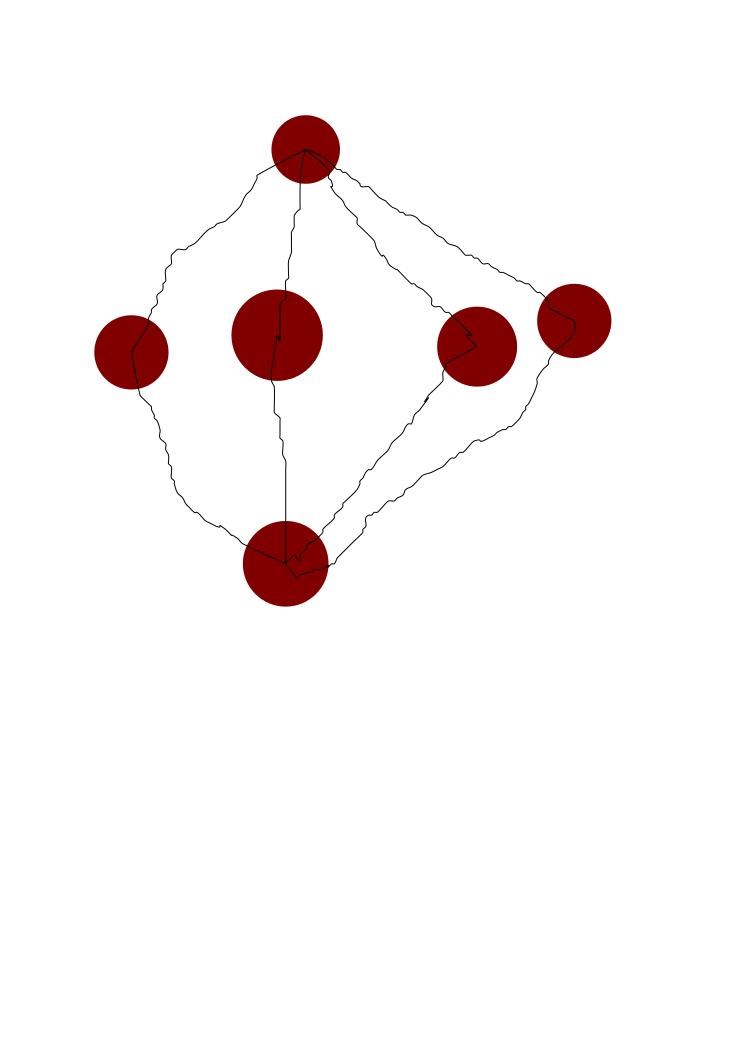
Villkor för att en graf ska ha en Eulerkrets och en Hamiltonkrets
Hej. Ja vad är villkoret? Jag vill bara ha ett svar rakt uppochned ifall någon vet om det. Jag har sökt på detta på engelska men hittar absolut ingenting.
Min fråga kommer ifrån en feltolkning av en fråga i boken. I boken stod det "vilket villkor gäller för att en graf ska ha både en eulerkrets och en hamiltonkrets?", de menade vad är villkoret för att varje eulerkrets i en graf samtidigt är en hamiltonkrets. Så tolkade jag inte frågan!
Varför går du över ån efter vatten? Enligt svenska Wikipedia är en Hamiltonväg en väg som passerar varje nod exakt en gång (och en Hamiltoncykel är en Hamiltonväg som börjar och slutar i samma nod), och en Eulerväg är en väg som passerar varje kant en gång, men den kan besöka samma nod flera gånger. Eller är det jag som har missförstått vad din fråga handlar om?
Ja, jag ver definitionerna av euler respektive hamiltonkrets, men vad krävs för att en given graf ska innehålla båda dessa?
https://sv.wikipedia.org/wiki/Hamiltongraf#Satser säger "Det finns än så länge inget ordentligt sätt att bevisa att det finns en Hamiltonväg i en graf."
Står frågan på engelska i boken?
Jag vet att det inte finns något sätt att bevisa det, men givet att det finns Eulerkretsar i grafen (alla hörn är jämna), vilka villkor gäller för att grafen även ska ha en hamiltonkrets?
Qetsiyah skrev:Jag vet att det inte finns något sätt att bevisa det, men givet att det finns Eulerkretsar i grafen (alla hörn är jämna), vilka villkor gäller för att grafen även ska ha en hamiltonkrets?
Det är inte så lätt. Det går att bevisa att vissa typer av grafer har en Hamiltonkrets, och då är det självklart ganska specifika sådana, men att visa att en godtycklig graf har en Hamiltonkrets är inte lätt.
EDIT: Läste inte så noga, sorry! Hur som helst så vet jag inget sätt att hitta/bevisa att en graf har en Hamiltonkrets bara för att den har en Eulerkrets. Om någon annan har bra koll får den gärna rätta mig.
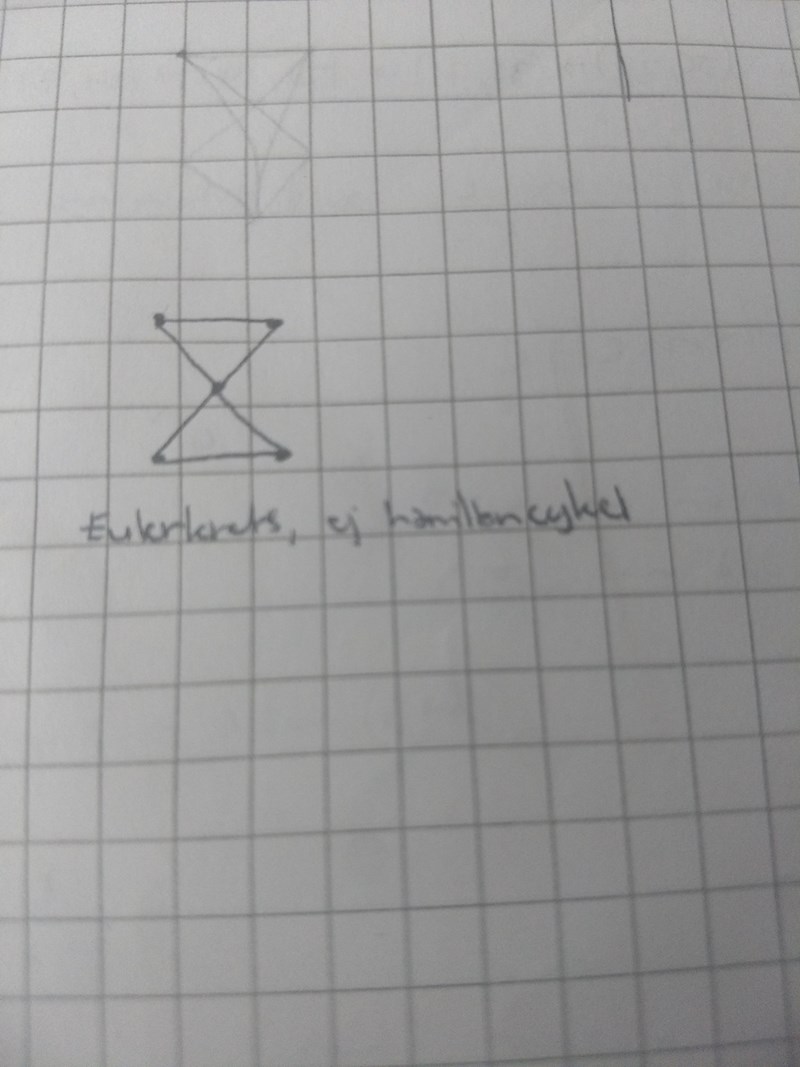
Jag har en obekräftad hypotes att om en graf ska ha både en Eulerkrets och en Hamiltoncykel måste den såklart ha endast jämna hörn (duh) och åtminstone "2-connectivity", alltså måste du ta bort åtminstone 2 hörn eller kanter för att grafen ska separeras. Jag tänker mig att om en graf har 1-connectivity kommer Hamiltonvägen inte kunna återvända till starten utan att passera ett hörn 2 gånger:
Kan någon bekräfta/motbevisa?
Moffen skrev:
visa att en godtycklig graf har en Hamiltonkrets är inte lätt.
Jag menar inte en godtycklig graf! Jag menar en graf vi redan vet har eulerkretsar.
1DumbTerrorist skrev:Jag har en obekräftad hypotes att om en graf ska ha både en Eulerkrets och en Hamiltoncykel måste den såklart ha endast jämna hörn (duh) och åtminstone "2-connectivity", alltså måste du ta bort åtminstone 2 hörn eller kanter för att grafen ska separeras. Jag tänker mig att om en graf har 1-connectivity kommer Hamiltonvägen inte kunna återvända till starten utan att passera ett hörn 2 gånger:
Kan någon bekräfta/motbevisa?
Jag håller med om att det är ett nödvändigt kriterium. Men jag har en annan eulersk graf som inte har en hamiltoncykel: