Vinkel
Om sin3x<1/2 och 0<x<pi/2 löser alla vinklar.
sin3x= 1/2
3x=pi/6+2n.Pi
x= pi/18+ (2/3) n.pi n all real nr
alltså 0<x<pi/18 0<x<10
men andra svaret 5pi/18<x<pi/2 50<x<90 jag kunde inte lösa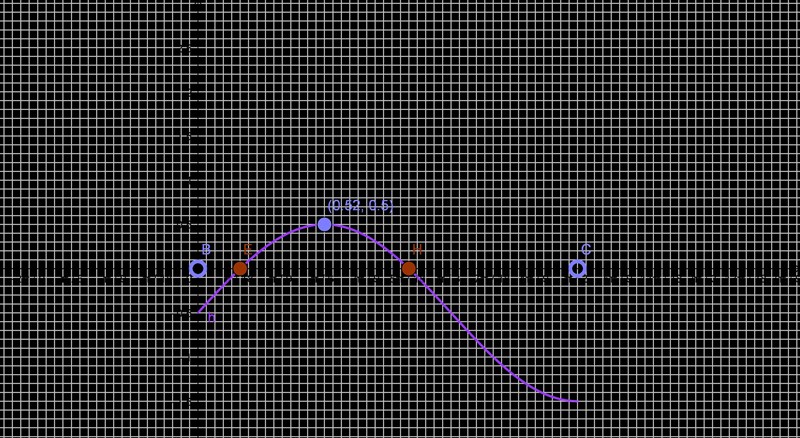
Tog bort dina versaler i rubriken. Det står i Pluggakutens regler (och i rutan där du skriver in din rubrik) att man skall undvika att skriva med endast stora bokstäver. /Smaragdalena, moderator
Rita upp enhets cirkeln, så ser du kanske att du måste kolla sin(pi/2-x) också
Vilken hemsk bild. Bra att du la in en bild förstås, men jag föredrar vit bakgrund och inte ett så finmaskigt rutnät.
RAWANSHAD skrev:Om sin3x<1/2 och 0<x<pi/2 löser alla vinklar.
sin3x= 1/2
3x=pi/6+2n.Pi
x= pi/18+ (2/3) n.pi n all real nr
alltså 0<x<pi/18 0<x<10
men andra svaret 5pi/18<x<pi/2 50<x<90 jag kunde inte lösa
Som du kan lösa om i detta avsnitt så har ekvationen lösningarna
och
Dividera med 3:
och
Kommer du vidare då?




