Vinkeln för moment
Hej.
På bilden nedan räknar dom infallsvinkeln mot momentet B som 2L * N * cos(v). Hur jag än sitter och vänder och vrider på trianglar förstår jag inte varför dom bytt ut sin(v) mot cos(v). Någon villig att förklara? Tack! 
Hur har du tänkt? har du ritat någon egen bild?
TeFy skrev:Hur har du tänkt? har du ritat någon egen bild?
För F har jag antagit att dom använder sig av dubbla vinklen för sinus. Om jag ritar en triangel så får jag det endast till att infallsvinkeln för N borde vara lika stor som planets lutning. Men det känns inte som det borde stämma.
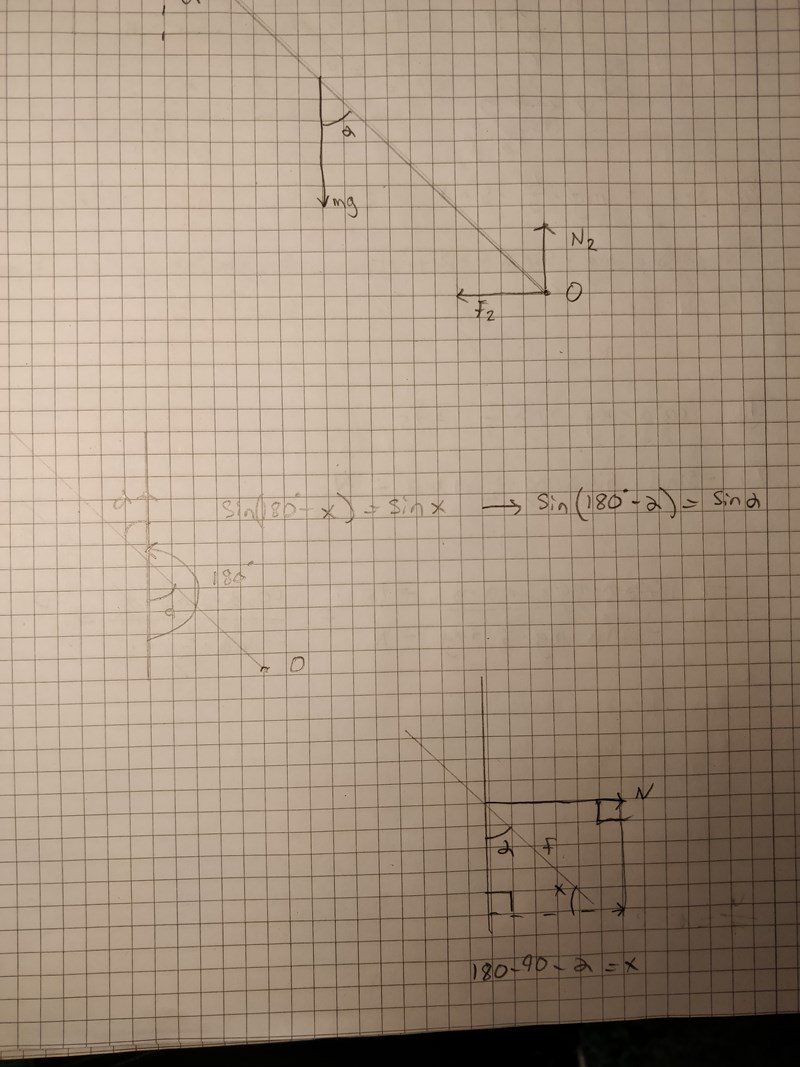
Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Rutger skrev:TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Vilket plan menar du?
2L*cos(phi) är momentaxeln för normalkraften. Är phi det du menar med v?
Laguna skrev:Rutger skrev:TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Vilket plan menar du?
2L*cos(phi) är momentaxeln för normalkraften. Är phi det du menar med v?
Ja
Laguna skrev:Rutger skrev:TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Vilket plan menar du?
2L*cos(phi) är momentaxeln för normalkraften. Är phi det du menar med v?
Plankan
Men du är med på varför det blir sinus för F och mg?
TeFy skrev:Men du är med på varför det blir sinus för F och mg?
Ja.
Om vi tänker så här då, F och N appliceras i samma punkt men är vinklade 90 grader mot varandra. Blir det något tydligare då?
Rutger skrev:Laguna skrev:Rutger skrev:TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Vilket plan menar du?
2L*cos(phi) är momentaxeln för normalkraften. Är phi det du menar med v?
Plankan
En kraft vinkelrät mot plankan får momentaxeln 2L, ja. Varför man ska skriva en faktor 1 som sin(90) vet jag inte.
Laguna skrev:Rutger skrev:Laguna skrev:Rutger skrev:TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Vilket plan menar du?
2L*cos(phi) är momentaxeln för normalkraften. Är phi det du menar med v?
Plankan
En kraft vinkelrät mot plankan får momentaxeln 2L, ja. Varför man ska skriva en faktor 1 som sin(90) vet jag inte.
Det ska man inte heller. Jag gav det som exempel, om N hade varit vinkrätt mot plankan. Alltså sin90. Min fråga består fortfarande var cos(phi) i N*L2*cos(phi) kommer ifrån. Hur kommer man fram till det?
Rutger skrev:Laguna skrev:Rutger skrev:Laguna skrev:Rutger skrev:TeFy skrev:Om jag förstår rätt så är det alltså de trigonometriska funktionerna i momentekvationen som förvirrar? Jag förstår inte riktigt var du menar att de byter sin(v) mot cos(v)
Ja. När dom räknar på vridmomentet för N. Hur kommer dom fram till att det är N *2L *cos(v)?
Jag förstår att N = kraften, 2l= längden. Men var kommer cos(v) ifrån?
Om N istället hade varit vinkelrät mot planet. Då hade man satt upp N*2L*sin(90).
Vilket plan menar du?
2L*cos(phi) är momentaxeln för normalkraften. Är phi det du menar med v?
Plankan
En kraft vinkelrät mot plankan får momentaxeln 2L, ja. Varför man ska skriva en faktor 1 som sin(90) vet jag inte.
Det ska man inte heller. Jag gav det som exempel, om N hade varit vinkrätt mot plankan. Alltså sin90. Min fråga består fortfarande var cos(phi) i N*L2*cos(phi) kommer ifrån. Hur kommer man fram till det?
Det skrev jag ju tidigare: 2L*cos(phi) är momentaxeln för normalkraften.
Den vinkel 90 grader som du tar sinus av i ditt exempel motsvarar inte phi. Phi är ganska liten, och om du gör den mindre och mindre så kommer du närmare ditt exempel. Det blir då cos(0) = 1 som är faktorn.


