Bestäm triangel
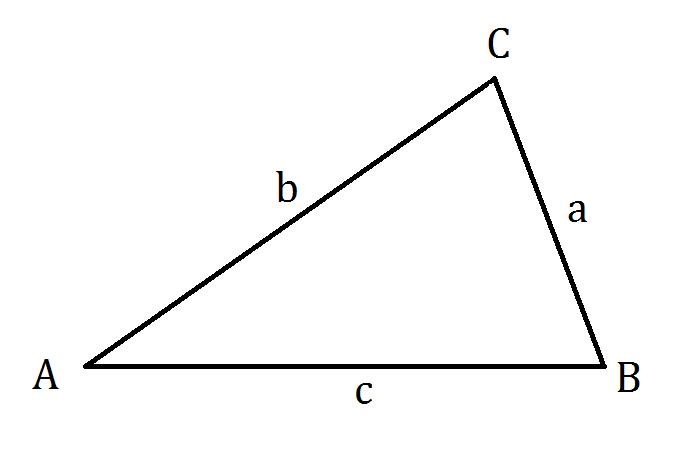
En triangel har vinklarna , och . Motstående sidor är , och , d.v.s. , och .
Det gäller att vinkeln . Sidan längdenheter (l.e.). Vidare är triangelns omkrets
l.e. FEL, se nedan /moderator
Bestäm vinklarna och de två okända sidorna i triangeln.
tomast80 bad att jag skall korrigera uttrycket för omkretsen: det skall vara . /Smaragdalena, moderator
Såg inget elegant sätt att presentera lösningen exakt så svaret får bli på decimalform.
Vår triangel är:
Om vi delar vinkeln B på mitten och drar en linje till sidan b får vi:
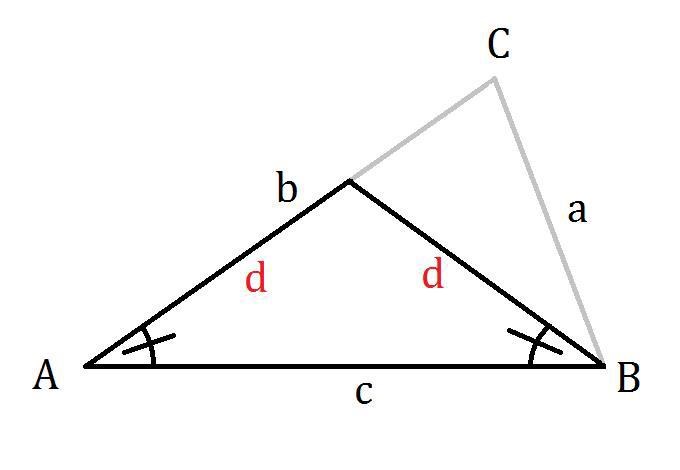
Vi ser här att vi kan få fram följande relation från denna triangel:
Om vi tittar på den triangel som bildades på högra sidan har vi:
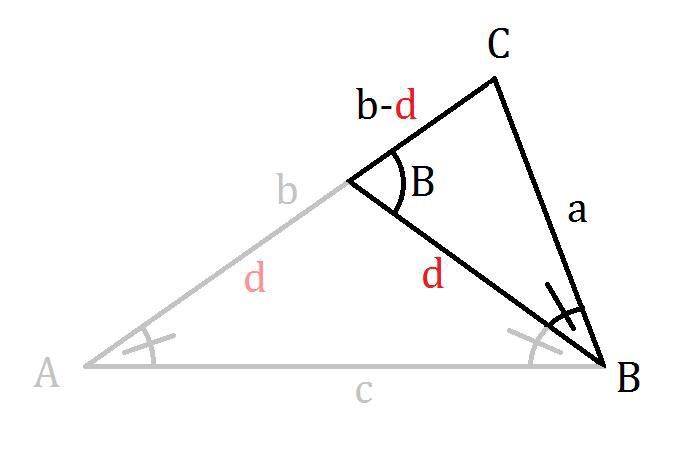
Denna är likformig med vår ursprungliga triangel så vi kan forma följande samband:
Vi har givet omkretsen och att sidan b = 5 vilket ger oss:
Kombinerar vi dessa tre resultat kan vi bestämma vinklarna:
Detta i sin tur ger med sinussatsen sidorna:
Hej Ebola!
Mycket snygg lösning! Tyvärr hade jag angett fel omkrets och bett ett antal moderatorer (för ett tag sen) att ändra mitt originalinlägg (låst efter 2 h). Hade hoppats att de skulle ändra FÖRE någon svarat på uppgiften. Nu blev det tyvärr inte så. Den rätta omkretsen ska vara:
Då får man exakta värden på vinklarna (uttryckt i grader) och även på sidorna.
Ursäkta för att du inte fick lösa uppgiften med rätt parametrar!
Om du orkar kan du ju se vad du får med rätt omkrets.
Oj, haha! Ja, så kan det gå. Lösningen är densamma så det gör inget för mig. Med rätt omkrets får jag vinklarna:
Vilket ger sidorna (i längdenheter):
Mycket vackert, Ebola!
En fundering bara, hur får du fram
?
är ju ingen standardvinkel.
Lite nyfiken.
tomast80 skrev:Mycket vackert, Ebola!
En fundering bara, hur får du fram
?
är ju ingen standardvinkel.
Lite nyfiken.
Av en ren slump har jag lagt den på minnet från grundkursen i matematik. Vi satt en afton och ställde upp formeln för halva vinkeln så vi kunde bestämma just cosd(15). Då var den i en annan form:
Det var en ren slump att jag såg det men hade annars bara använt miniräknare. Om inte miniräknare var tillåtet hade jag sannolikt inte ens gått denna rutt utan jag hade behövt gå en längre väg för att identifiera uttryck för alla vinklar och hoppas att någon av dem utgör standardvinklar. I detta fall är både B och C sådana.
Hej igen!
Vilket roligt sammanträffande!
Jag hade nog chansat på att vinkeln var ”enklare” att få fram och använt formeln för dubbla vinkeln.
Här är en annan lösningsmetod:
Sinussatsen ger:
ur vilket det ganska enkelt följer att
och
Omkretsen kan därför uttryckas enligt:
Då ett uttryck för omkretsen är känt gäller det bara att ta uttrycka kvoterna och i enbart en av vinklarna. Vi väljer . Vi får att:
och
Om man inte redan känner till uttrycket kan detta härledas ganska smärtfritt med Eulers formel:
Visa spoiler
Betrakta talet
Vi kan även uttrycka detta som:
Likaställs imaginärdelarna från de två uttrycken erhålls:
Detta uttryck ger:
Sätter vi in detta i vårt uttryck för fås:
Använder vi nu det givna uttrycket för omkretsen och sätter in får vi:
Härifrån kan man som redan diskuterats antingen känna igen rotuttrycket som eller istället lösa ut för som tomast visade. Man får då till slut:
Mycket vackert AlvinB! Jag löste den på samma sätt m.h.a. sinussatsen. Roligt att det fanns helt olika typer av lösningar på denna uppgift, det hade jag inte koll på när jag konstruerade uppgiften.




