vinkler

Hej, här är frågan, det som jag undrar på är hur kan man beräkna intervallet för vinklerna när vi byter till sfäriska koordinater 

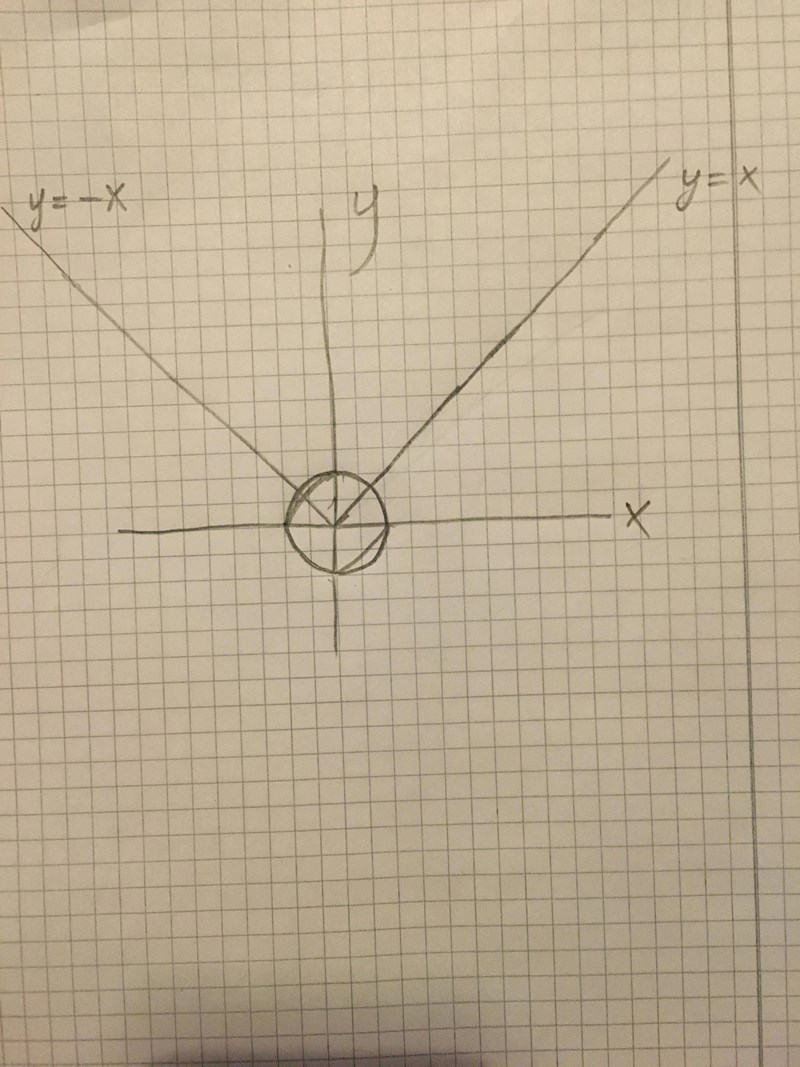
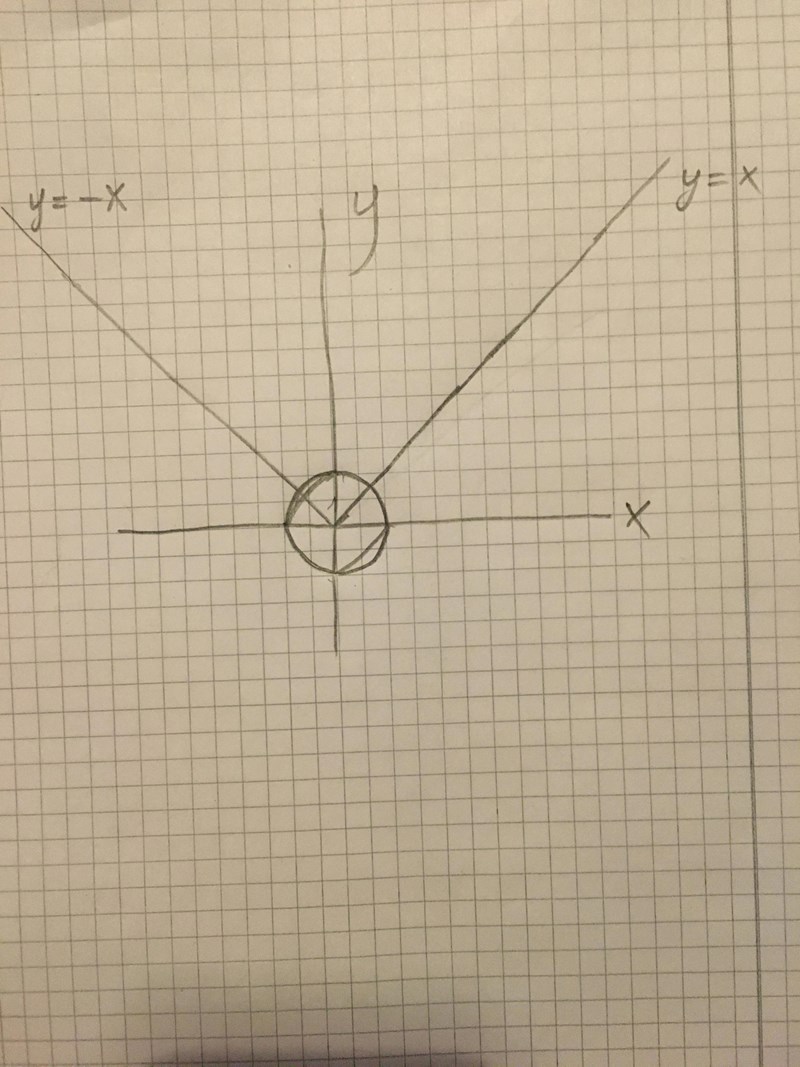
Den är ganska snäll, så du kan rita upp ett plan i taget. Först får du radien från klotet, sen ritar du upp den andra funktionen i samma bild som en enhetscirkel och får nästa vinkel. Till slut kan du strunta i y och rita upp konen med bara x och z på axlarna så har du den sista.

hej, och tack för din svar, radien är 1, kan du förklara lite mera hur jag ska rita området

Rita bara y>|x| först, likadant som du hade gjort på gymnasiet. Rita sen in en enhetscirkel i bilden och visa vad du får.

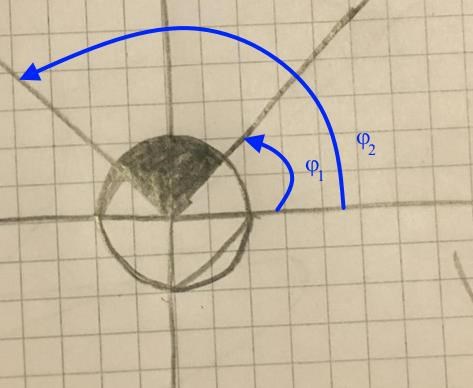
Precis. Du vill ha den lilla triangel-liknande biten högst upp. Vinka vinklar har kanterna till den?

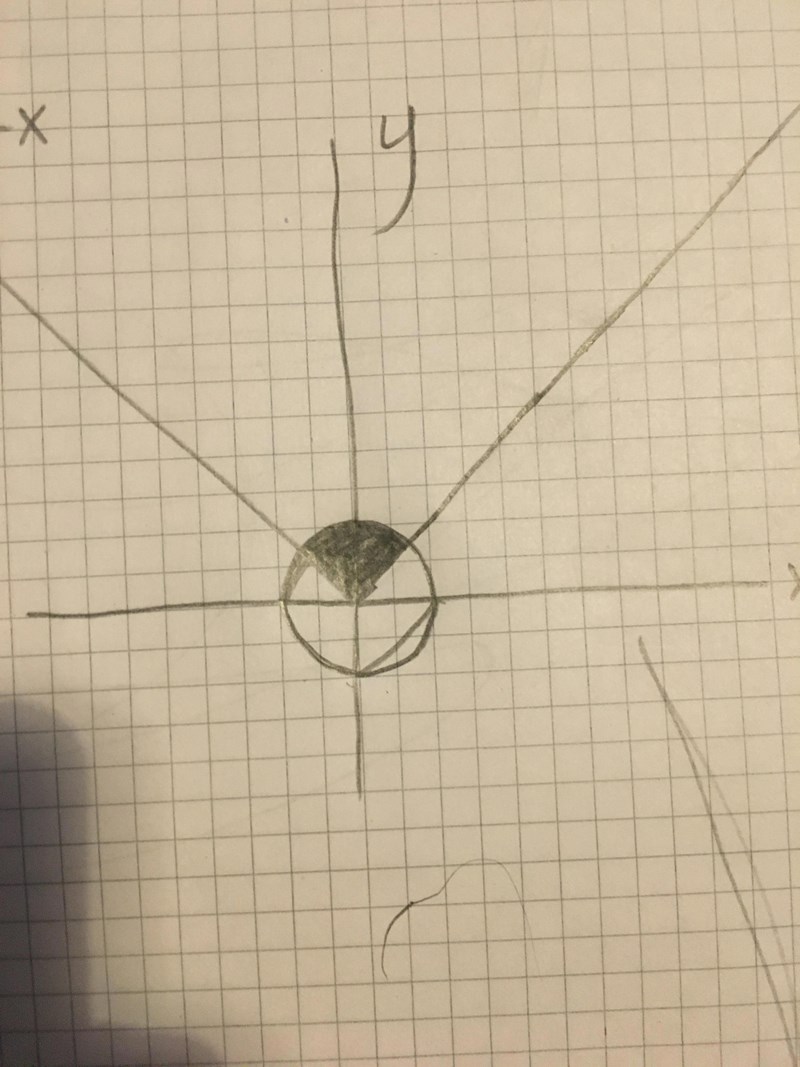
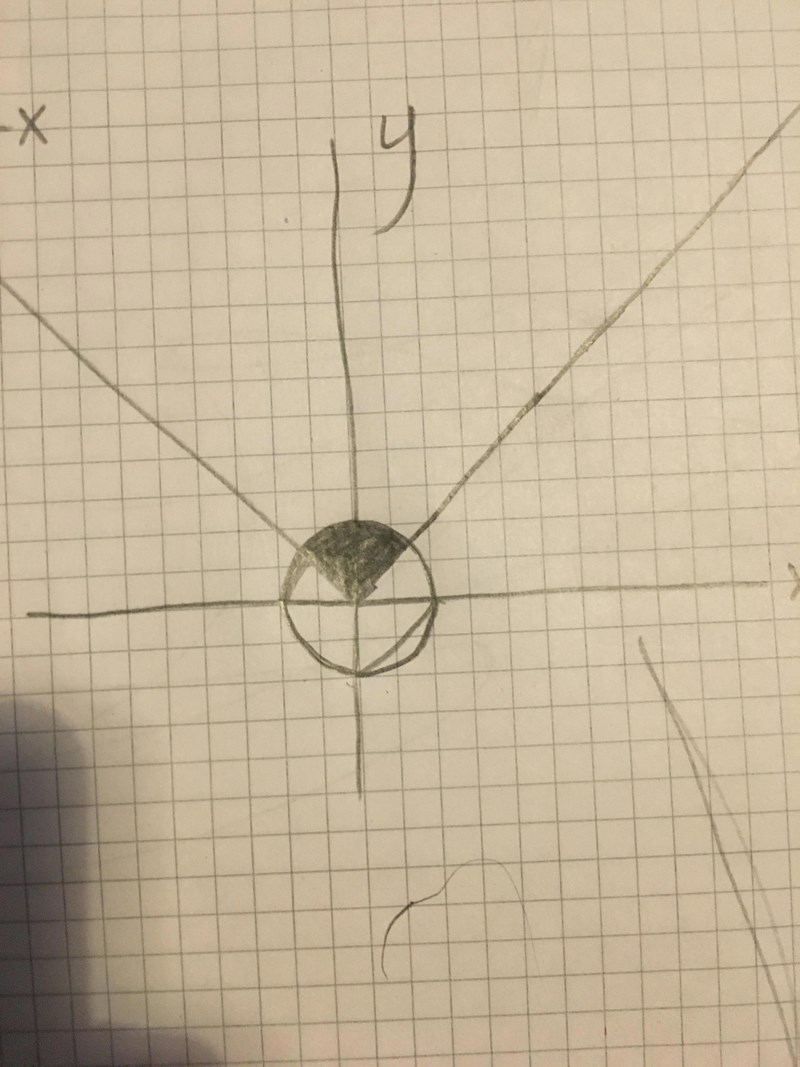
Hej, är det den här triangelen, och vad menas med vinka vinklar

$\varphi_1=?$

$\varphi_2=?$

φ1= från 0 till pi/4

φ2= från  0 till 3pi/4

Just det, så för det svarta området gäller $\varphi\in [\varphi_1, \varphi_2]$

Dvs, gränserna för $\varphi$:

$\frac{\pi}{4}<\varphi<\frac{3\pi}{4}$

Kan du räkna ut gränserna för $\theta$ också?

Använd $z=r\cos(\theta)$

$z\leq \sqrt{x^2+y^2} \Rightarrow \quad ?$

hej, igen men vad menar du med rightleftarrow

Jag har rättat till mitt inlägg nu, det blev fel i Latex.

Du har räknat ut gränserna för vinkeln $\varphi$ i xy-planet.

Nästa steg är att räkna ut gränserna för vinkeln $\theta$ mot z-axeln.

kan vi använde att sqrt(x^2+y^2) =r och att detta medför att cos(θ) =1 , men då är vinkeln lika med antingen noll eller pi

Tänk på att i sfäriska koordinater (3 koordinater, x,y,z) är $\sqrt{x^2+y^2}=r\sin(\theta)$

Alltså är $z\leq \sqrt{x^2+y^2} \iff r\cos(\theta)\leq r\sin(\theta)$

Hej, är detta rät

Njäe. Det är ingen ekvation. det är en olikhet

$r\cos(\theta)\leq r\sin(\theta)$

Dela båda sidor med r.

$\cos(\theta)\leq \sin(\theta)$

Dela båda sidor med $\cos(\theta)$

$1\leq\tan(\theta)$

$\theta\geq \frac{\pi}{4}$

Så $\theta \in[\pi/4, \pi]$

dvs gränserna för $\theta$ är $\frac{\pi}{4}<\theta<\pi$

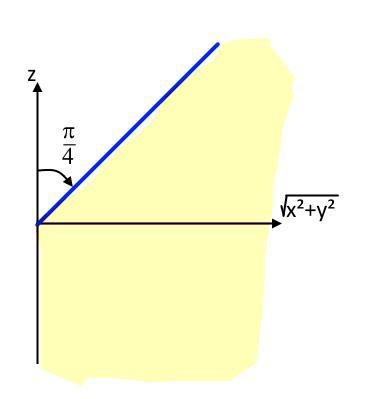
I det gula området är $z\leq \sqrt{x^2+y^2}$

Tack så mycket, men betyder detta att vinkelen börjar från pi/4 till pi. Men hur ser vi att den ska ha pi värdet också .

skulle vinkelen inte vara lik noll då den är lika med sqrt(x^2+y^2)-axeln 

Nej, du börjar inte alltid på 0, här har vi ett klot utan översta biten, så då måste vi börja på den vinkeln där figuren börjar. Om jag fattade frågan rätt?

Hej, jag tänkte nämligen på hur vi kommer fram till att vinkelen ska vara från pi/4 till pi. Vi kom fram till att den börjar från pi/4. Men hur ser vi till exempel på figuren, eller beräknar att den ska vara mindre än pi. 
mvh

suad 

Eftersom det inte finns någon undre gräns i olikheten kan vinkeln gå hela vägen ner till pi, och då pekar den rakt nedåt så längre än så går aldrig komma i sfäriska koordinater.

Hej, och tack för din hjälp, nu forstod jag, vinkelen får inte vara större än pi. Därmed ligger den mellan pi/4 och pi.

hej, igen i ett annat fråga får jag detta området, x^2+y^2+z^2=4, 3z^2=x^2+y^2, z>=0. så jag vet från klotet att radien är 2.  och när vi byter till sfäriska koordinater får vi att vinkelen 0<φ<2pi. och att 0<θ<pi/3. men när jag använder att z=0 och att z=Rcosθ och lösar att cosθ=0, men får att θ=pi/2, så det är inte rätt, och även då jag använder att z=1/sqrt(3)*sqrt(x^2+y^2) som då ger att sqrt(x^2+y^2)=sqrt(3)*Rsinθ. och sätter att Rcosθ=sqrt(3)*Rsinθ får jag också fel, kan jag få hjälp så att jag får rätt intervall

Uppgift 7

suad, gör en ny tråd för den nya frågan, det blir så rörigt annars. /moderator

tack, det ska jag göra