Visa att 7 är en delare

Bra än så länge! Vi kan skriva om uttrycken genom att byta bas . Exempelvis genom att skriva om $3^{11} = 3 \cdot 3^{10} = 3 \cdot 9^5$.

Eftersom $9 \equiv 2 \,\pmod 7$ har vi att

$3^{11} =3\cdot 9^5 \equiv 3 \cdot 2^5 \equiv 3 \cdot 32 \,\pmod 7$.

Kan du göra något liknande för $5^{13}$?

Här fick jag stopp

Bra!

Ned till $5^1 \cdot 4^6$ är det rätt. Det bör vara $2^3$ i den sista raden, då $4^6 = 16^3 \equiv 2^3 \, \pmod 7$.

Men nu har du ett litet tal! $5 \cdot 2^3 = 40$. Tillsammans med resten för $3^{11}$, hur förenklas resten för $(3^{11} + 5^{13})^9$?

jag vet inte hur jag ska forsätta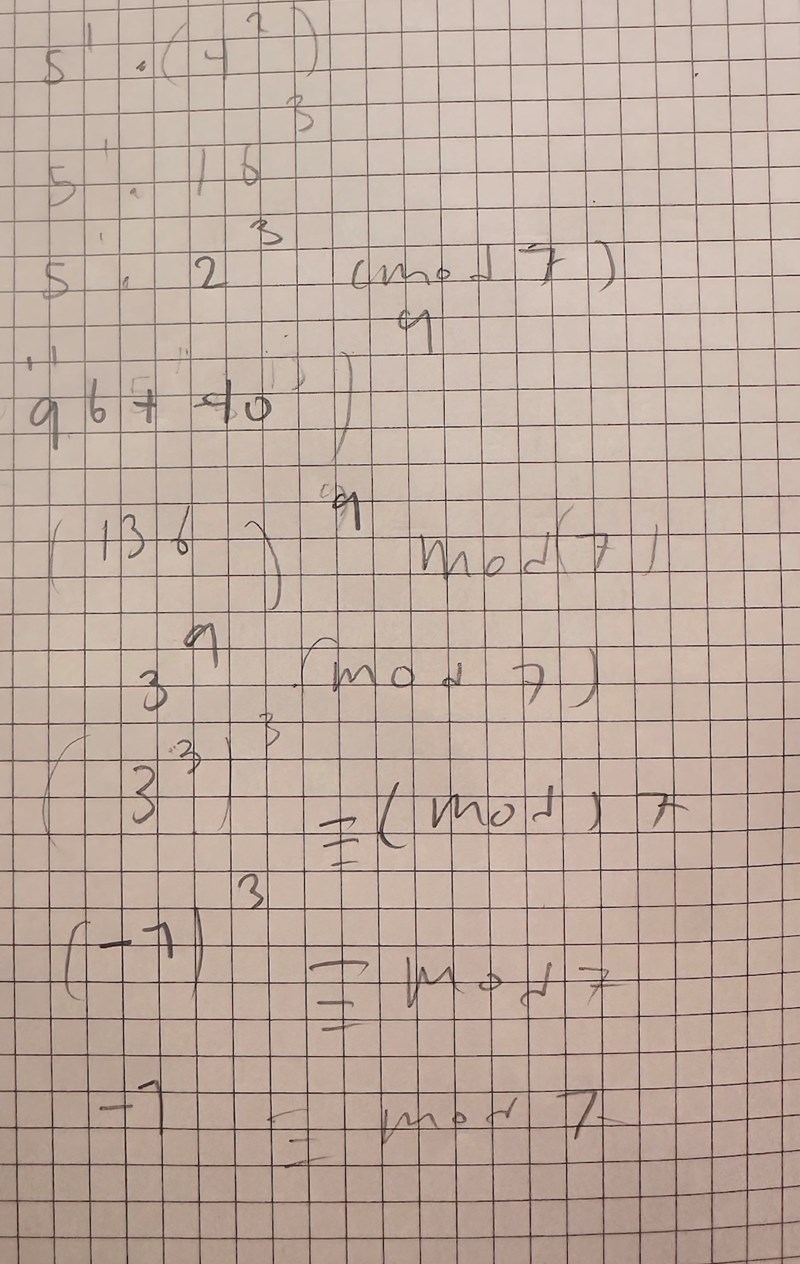 

Du har alltså att $(31^{11}+19^{13})^9 \equiv -1\, \pmod {7}$

Addera 1 till båda led och få $(31^{11}+19^{13})^9 + 1 \equiv 0\, \pmod {7}$