20 svar

593 visningar

AlexMu behöver inte mer hjälp

Visa att alla* rötter till en polynomekvation har absolutbelopp mindre än 1.

Halloj!

Jag har hållit på med ett problem jag hittade på.

Det enda jag har kvar att göra är att visa att alla lösningar (reella och komplexa) till ekvationen

$x^k - x^{k-1} -\dots-x-1=0$ (för något positivt heltal $k$ )

har absolutbelopp mindre 1 förutom en, och den är reell och positiv. Detta är något jag aldrig gjort och vet inte riktigt hur man ska tänka gällande det.

Visserligen kan man skriva om de negativa termerna som en geometrisk talserie. Detta gör om ekvationen till

$\displaystyle x^k - \frac{x^k-1}{x-1}=0$

Multiplikation av $x-1$ introducerar den extra roten $x=1$ .

Vi får, efter lite omskrivning

$x^{k+1}-2x^k+1 = 0$ , $x\neq 1$ , som då har samma rötter som den tidigare.

Hur visar man något sådant här?

Resten av mitt inlägg handlar om vart detta kommer ifrån (inte relevant till min själva fråga, däremot tycker jag det är intressant).

Fibonaccis talföljd definieras enligt rekursionen

$\displaystyle F_n = F_{n-1} + F_{n-2}$ (och några startvärden, typ $F_0 = 1$ , $F_1 = 1$ )

Oberoende startvärden gäller det att

$\displaystyle \lim_{n \to \infty}{\frac{F_{n+1}}{F_n}} = \frac{1+\sqrt 5}{2}$

Det som är mer intressant är att gränsvärdet är den positiva roten till ekvationen $x^2 - x - 1 =0$ . Man kan visa detta på massvis med olika sätt, den jag själv tycker om mest är att utvidga bråket på ett roligt sätt (i spoilern):

Visa spoiler

Skriv om bråket såhär:

\displaystyle \frac{F_{n+1}}{F_{n}} = \frac{F_n + F_{n-1}}{F_n} =1 + \frac{F_{n-1}}{F_n} = 1+ \frac{F_{n-1}}{F_{n-1}+F_n}

Dividera nu täljare och nämnare med

F_{n-1}

\displaystyle = 1 + \frac{1}{\frac{F_{n-1}+F_n}{F_{n-1}}} =1 + \frac{1}{1+\frac{F_n}{F_{n-1}}}

Sedan fortsätter man detta rekursivt. Låt

a_n = \frac{F_{n+1}}{F_n}

. Då uppfyller

a_n

rekursionen

\displaystyle a_{n+1} = 1 + \frac 1{a_n}

Låt

\lim_{n\to \infty} a_n =L

(Efter man har visat att

\lim a_n

konvergerar)

Då har vi att

\lim_{n\to \infty}a_n = \lim_{n\to \infty}\left(1+\frac{1}{a_{n-1}}\right)

. Uppenbart spelar den där

n-1

ingen roll när

n \to \infty

, så vi har:

\displaystyle L = 1 + \frac 1L

, vilket ger oss ekvationen

L^2 - L - 1=0

.
Denna ekvation har den positiva lösningen

\displaystyle L = \frac{1 +\sqrt 5}2

Jag vill undersöka på talföljder på formen

$a_n = a_{n-1} + a_{n-2} + \dots + a_{n-k}$ för något positivt heltal $k$ , där $a_0=a_1=a_2=\dots=a_{k-1}=1$ (detta verkar inte spela någon roll för mina ändamål)

Numeriskt verkar det alltid vara så att $\displaystyle \lim_{n\to \infty}{\frac{a_{n+1}}{a_n}}$ är den positiva roten till ekvationen

$x^k - x^{k-1}- x^{k-2}-\dots - x^2 - x - 1=0$

Exempel för $k=3$ och $k=5$ :

Det jag vill göra är att visa att detta stämmer. Min ide baseras på en övning i en bok jag läste för några månader sedan:
I nästa övning generaliseras detta från en rekursion av 2 föregående tal till $k$ föregående.

(Såhär ser den övningen ut)

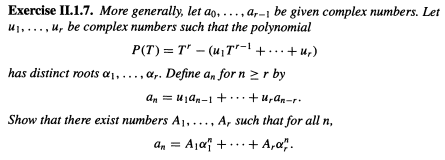
Därför vet vi att vi kan skriva $a_n$ som

$a_n = A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n$

Där $\alpha_i$ är rötterna till $x^k - x^{k-1}-\dots-x-1=0$ och där $\alpha_1$ är den största reella roten (existensen av denna är då del av min fråga).

Då reduceras problemet till att visa att

$\displaystyle \lim_{n\to \infty}{\frac{A_1\alpha_1^{n+1} +A_2\alpha_2^{n+1} +\dots+ A_k\alpha_k^{n+1}}{A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n}} = \alpha_1$

Vi kan skriva om argumentet i gränsvärdet genom att addera och subtrahera $\alpha_1\left(A_2 \alpha_2^n +\dots+A_{k} \alpha_{k}^n\right)$

$\displaystyle \frac{A_1\alpha_1^{n+1} +A_2\alpha_2^{n+1} +\dots+ A_k\alpha_k^{n+1}}{A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n}$

$\displaystyle = \frac{A_1\alpha_1^{n+1} + \alpha_1\left(A_2 \alpha_2^n +\dots+A_{k} \alpha_{k}^n\right)-\alpha_1\left(A_2 \alpha_2^n +\dots+A_{k} \alpha_{k}^n\right) +A_2\alpha_2^{n+1} +\dots+ A_k\alpha_k^{n+1}}{A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n}$

Faktorisering av de första $k$ termerna ger

$\displaystyle = \frac{\alpha_1\left(A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n\right)-\alpha_1\left(A_2 \alpha_2^n +\dots+A_{k} \alpha_{k}^n\right) +A_2\alpha_2^{n+1} +\dots+ A_k\alpha_k^{n+1}}{A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n}$

$\displaystyle = \alpha_1 + \frac{-\alpha_1\left(A_2 \alpha_2^n +\dots+A_{k} \alpha_{k}^n\right) +A_2\alpha_2^{n+1} +\dots+ A_k\alpha_k^{n+1}}{A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n}$

Då blir målet att visa att gränsvärdet av bråket är 0. Efter lite omskrivning av bråket får vi:

$\displaystyle \frac{A_2\alpha_2^n\left(\alpha_2 - \alpha_1\right)+\dots +A_k\alpha_k^n\left(\alpha_k - \alpha_1\right)}{A_1\alpha_1^n +A_2\alpha_2^n +\dots+ A_k\alpha_k^n}$

Det intressanta är att varje term i täljaren är en faktor av $\alpha_j^n$ där $j > 1$

Om vi låter $k=3$ och kollar på rötterna ser vi:

Som vi ser här har de två komplexa rötterna (lila) absolutbelopp mindre än 1. Därför borde $\alpha_2^n$ och $\alpha_3^n$ gå mot $0$ när $n\to \infty$ . Alltså går täljaren mot 0 samtidigt som nämnaren inte gör det då vi även har $A_1 \alpha_1^n$ -termen där. Därmed går hela bråket mot 0.

Då återstår det bara att visa att alla rötter till

$x^k - x^{k-1} -\dots-x-1=0$

förutom 1, som är reell och positiv, har absolutbelopp mindre än 1.

Detta verkar stämma, exempel för $k = 6$ och $k = 20$ :

Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

AlexMu skrev:
Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

Kjell var (och är) en mycket trevlig person. Det finns många skarpa personer på Matte/Lund, men det krävs uthållighet att göra det i 30 år... I början var nog Petree, Meurmann och Wanby också med och svarade men navet har alltid varit Kjell.

Det är en fin källa för olika problem. Mycket att läsa. Lite tråkigt HTMLformat, men det får man ta.

Då återstår bara StackExchange. Eftersom du gör grundligt förarbete kommer du inte få några problem att få svar. Det finns mycket kunnigt folk där som säkert vet svaret direkt.

Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

Kjell var (och är) en mycket trevlig person. Det finns många skarpa personer på Matte/Lund, men det krävs uthållighet att göra det i 30 år... I början var nog Petree, Meurmann och Wanby också med och svarade men navet har alltid varit Kjell.

Det är en fin källa för olika problem. Mycket att läsa. Lite tråkigt HTMLformat, men det får man ta.

Då återstår bara StackExchange. Eftersom du gör grundligt förarbete kommer du inte få några problem att få svar. Det finns mycket kunnigt folk där som säkert vet svaret direkt.

Ja, tack så mycket för länken!

MathSE är en sida jag gillar att läsa frågor och svar på, men har alltid undvikt att lägga upp mina egna frågor på grund av ryktet gällande StackExchange-sidor lol. Men du har nog rätt, kan ta och skriva en fråga där imorgon (och hoppas att jag skriver den bra nog för dem).

AlexMu skrev:
Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

Kjell var (och är) en mycket trevlig person. Det finns många skarpa personer på Matte/Lund, men det krävs uthållighet att göra det i 30 år... I början var nog Petree, Meurmann och Wanby också med och svarade men navet har alltid varit Kjell.

Det är en fin källa för olika problem. Mycket att läsa. Lite tråkigt HTMLformat, men det får man ta.

Då återstår bara StackExchange. Eftersom du gör grundligt förarbete kommer du inte få några problem att få svar. Det finns mycket kunnigt folk där som säkert vet svaret direkt.

Ja, tack så mycket för länken!

MathSE är en sida jag gillar att läsa frågor och svar på, men har alltid undvikt att lägga upp mina egna frågor på ryktet gällande StackExchange-sidor lol. Men du har nog rätt, kan ta och skriva en fråga där imorgon (och hoppas att jag skriver den bra nog för dem).

MathSE är beryktat för sin hårda ton :) Men det är bara om man skriver "Hur löser man...?". Presenterar man problemet och gör en ansats haglar hjälpen in. Du har inget att frukta där. Läx-latmaskar bör hålla sig därifrån :)

Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

Kjell var (och är) en mycket trevlig person. Det finns många skarpa personer på Matte/Lund, men det krävs uthållighet att göra det i 30 år... I början var nog Petree, Meurmann och Wanby också med och svarade men navet har alltid varit Kjell.

Det är en fin källa för olika problem. Mycket att läsa. Lite tråkigt HTMLformat, men det får man ta.

Då återstår bara StackExchange. Eftersom du gör grundligt förarbete kommer du inte få några problem att få svar. Det finns mycket kunnigt folk där som säkert vet svaret direkt.

Ja, tack så mycket för länken!

MathSE är en sida jag gillar att läsa frågor och svar på, men har alltid undvikt att lägga upp mina egna frågor på ryktet gällande StackExchange-sidor lol. Men du har nog rätt, kan ta och skriva en fråga där imorgon (och hoppas att jag skriver den bra nog för dem).

MathSE är beryktat för sin hårda ton :) Men det är bara om man skriver "Hur löser man...?". Presenterar man problemet och gör en ansats haglar hjälpen in. Du har inget att frukta där. Läx-latmaskar bör hålla sig därifrån :)

Det är sant. Deras ton har gjort mig lite rädd för sidan, men samtidigt förstår jag verkligen att de är hårda mot lite lata frågor. Det är inte särskilt ovanligt här att se inlägg där bilderna är upp och ned eller något liknande. Jag tycker dock att de på MathSE kan vara för hårda mot folk, vilket är synd.

AlexMu skrev:
Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

Kjell var (och är) en mycket trevlig person. Det finns många skarpa personer på Matte/Lund, men det krävs uthållighet att göra det i 30 år... I början var nog Petree, Meurmann och Wanby också med och svarade men navet har alltid varit Kjell.

Det är en fin källa för olika problem. Mycket att läsa. Lite tråkigt HTMLformat, men det får man ta.

Då återstår bara StackExchange. Eftersom du gör grundligt förarbete kommer du inte få några problem att få svar. Det finns mycket kunnigt folk där som säkert vet svaret direkt.

Ja, tack så mycket för länken!

MathSE är en sida jag gillar att läsa frågor och svar på, men har alltid undvikt att lägga upp mina egna frågor på ryktet gällande StackExchange-sidor lol. Men du har nog rätt, kan ta och skriva en fråga där imorgon (och hoppas att jag skriver den bra nog för dem).

MathSE är beryktat för sin hårda ton :) Men det är bara om man skriver "Hur löser man...?". Presenterar man problemet och gör en ansats haglar hjälpen in. Du har inget att frukta där. Läx-latmaskar bör hålla sig därifrån :)

Det är sant. Deras ton har gjort mig lite rädd för sidan, men samtidigt förstår jag verkligen att de är hårda mot lite lata frågor. Det är inte särskilt ovanligt här att se inlägg där bilderna är upp och ned eller något liknande. Jag tycker dock att de på MathSE kan vara för hårda mot folk, vilket är synd.

Det känns som om det är moderatorerna där som är hårda. De som är hjälpsamma brukar inte vara stränga, tvärt om. Jag tror moderatorernas attityd har varit uppe för allmän diskussion för ett par år sedan då många tyckte att det gick för långt. Jag har inte varit där så många år så jag kan säga något om hur det utvecklats under åren. Jag har postat några frågor och fått "poäng" och "up-vote" för frågeformulering. Jag har också fått några "Det där har vi pratat om tidigare, STÄNGD!", fast det var på Mathematica-sidan, inte matte. Jag tycker de är hårdare på Mathematica-sidan än matte, men om presentationen är bra så nappar många och moderatorerna håller sig borta :)

Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
AlexMu skrev:
Trinity2 skrev:
Passa på och fråga

https://www1.maths.lth.se/query/

innan Kjell går i pension (=snart). Han har gjort en fantastisk insats och han är enormt kunnig. Det är synd att ingen tar vid.

Verkar tyvärr redan vara för sent..

Tack för länken dock! Verkar finnas mycket intressanta frågor och svar där!

Kjell var (och är) en mycket trevlig person. Det finns många skarpa personer på Matte/Lund, men det krävs uthållighet att göra det i 30 år... I början var nog Petree, Meurmann och Wanby också med och svarade men navet har alltid varit Kjell.

Det är en fin källa för olika problem. Mycket att läsa. Lite tråkigt HTMLformat, men det får man ta.

Då återstår bara StackExchange. Eftersom du gör grundligt förarbete kommer du inte få några problem att få svar. Det finns mycket kunnigt folk där som säkert vet svaret direkt.

Ja, tack så mycket för länken!

MathSE är en sida jag gillar att läsa frågor och svar på, men har alltid undvikt att lägga upp mina egna frågor på ryktet gällande StackExchange-sidor lol. Men du har nog rätt, kan ta och skriva en fråga där imorgon (och hoppas att jag skriver den bra nog för dem).

MathSE är beryktat för sin hårda ton :) Men det är bara om man skriver "Hur löser man...?". Presenterar man problemet och gör en ansats haglar hjälpen in. Du har inget att frukta där. Läx-latmaskar bör hålla sig därifrån :)

Det är sant. Deras ton har gjort mig lite rädd för sidan, men samtidigt förstår jag verkligen att de är hårda mot lite lata frågor. Det är inte särskilt ovanligt här att se inlägg där bilderna är upp och ned eller något liknande. Jag tycker dock att de på MathSE kan vara för hårda mot folk, vilket är synd.

Det känns som om det är moderatorerna där som är hårda. De som är hjälpsamma brukar inte vara stränga, tvärt om. Jag tror moderatorernas attityd har varit uppe för allmän diskussion för ett par år sedan då många tyckte att det gick för långt. Jag har inte varit där så många år så jag kan säga något om hur det utvecklats under åren. Jag har postat några frågor och fått "poäng" och "up-vote" för frågeformulering. Jag har också fått några "Det där har vi pratat om tidigare, STÄNGD!", fast det var på Mathematica-sidan, inte matte. Jag tycker de är hårdare på Mathematica-sidan än matte, men om presentationen är bra så nappar många och moderatorerna håller sig borta :)

Ja, det där med ”this question is a duplicate” är intressant. Jag kanske bara är dålig på att söka på den sidan, men ofta lyckas jag inte hitta de gamla svaren om jag letar själv.

Jag har skrivit en fråga på MathSE, och generellt var svaren trevliga och bra. Däremot kom det en sådan där ”duplicate” kommentar. Höll inte riktigt med om att det var samma fråga, då jag frågade om man kunde förenkla en summa ytterligare, medan svaret på den andra frågan var den summan jag frågade om. Däremot vet jag att jag inte såg det inlägget när jag sökte efter liknande frågor innan jag gjorde min egen.

Ja, det där med ”this question is a duplicate” är intressant. Jag kanske vara är dålig på att söka på den sidan, men ofta lyckas jag inte hitta de gamla svaren om jag letar själv.

Jag har skrivit en fråga på MathSE, och generellt var svaren trevliga och bra. Däremot kom det en sådan där ”duplicate” kommentar. Höll inte riktigt med om att det var samma fråga, då jag frågade om man kunde förenkla en summa ytterligare, medan svaret på den andra frågan var den summan jag frågade om. Däremot vet jag att jag inte såg det inlägget när jag sökte efter liknande frågor innan jag gjorde min egen.

Sökmotorer är ofta undermåliga. Är man inte inföding heller känner man inte till de subtila nyanserna i språket som gör frågan "bättre" för motorn. Dessutom har matematik en speciell jargong som inte är så lätt att hantera. T.ex. skulle jag vara helt förvirrad inom abstrakt algebra och dess terminologi.

Din fråga ser ju utmärkt ut och 8 up-vote. Kör på!

Trinity2 skrev:
Ja, det där med ”this question is a duplicate” är intressant. Jag kanske vara är dålig på att söka på den sidan, men ofta lyckas jag inte hitta de gamla svaren om jag letar själv.

Jag har skrivit en fråga på MathSE, och generellt var svaren trevliga och bra. Däremot kom det en sådan där ”duplicate” kommentar. Höll inte riktigt med om att det var samma fråga, då jag frågade om man kunde förenkla en summa ytterligare, medan svaret på den andra frågan var den summan jag frågade om. Däremot vet jag att jag inte såg det inlägget när jag sökte efter liknande frågor innan jag gjorde min egen.

Sökmotorer är ofta undermåliga. Är man inte inföding heller känner man inte till de subtila nyanserna i språket som gör frågan "bättre" för motorn. Dessutom har matematik en speciell jargong som inte är så lätt att hantera. T.ex. skulle jag vara helt förvirrad inom abstrakt algebra och dess terminologi.

Din fråga ser ju utmärkt ut och 8 up-vote. Kör på!

Skriver en fråga där imorgon. Tack för diskussionen här!

Spännande fråga! Här kommer lite lösa första observationer som inte svarar på din fråga, men som kanske ändå är viktiga att etablera för att vi ska kunna resonera vidare.

Låt oss införa notationen $p_k(x)=x^k-x^{k-1}-x^{k-2}-\cdots-x-1$ , och $q_k(x)=(x-1)p_k(x)=x^{k+1}-2x^k+1$ .

Vi kan börja med att konstatera att alla komplexa rötter av $q_k$ (och därmed också $p_k$ ) har multiplicitet 1, eftersom $q_k(x)$ och derivatan $q_k'(x)$ inte har några gemensamma rötter. Så totalt kommer $p_k(x)$ att ha $k$ komplexa rötter enligt algebrans fundamentalsats.

Låt oss nu fundera på de reella rötterna:

Genom en kombination av Descartes teckenregel och att explicit titta på derivatorna tycker jag mig kunna sluta mig till att det finns en eller två reella rötter för alla $k>0$ .
Det finns alltid en unik positiv rot. Denna rot ligger på intervallet $(1,2)$ , och konvergerar mot $2$ när $k\to\infty$ .
Om $k$ är jämnt finns det dessutom en unik negativ rot. Den ligger på intervallet $(-1,0)$ och konvergerar mot $-1$ när $k\to\infty$ .

Jag får fundera vidare på de icke-reella rötterna...

För skojs skull plottade jag alla rötterna till $q_k(x)$ i WolframAlpha för olika $k$ , vilket verkar stöjda observationerna ovan och din huvudsakliga förmodan. Så här ser det t.ex. ut för $k=15$ :

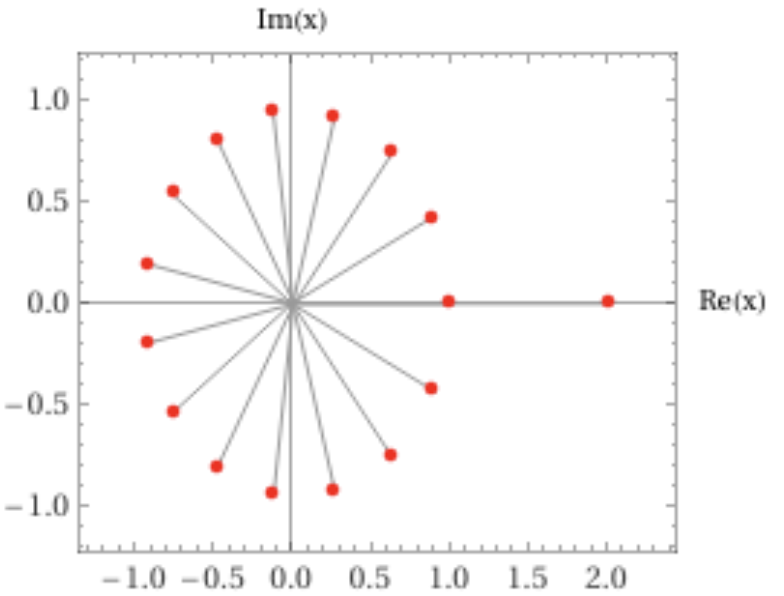
Ytterligare en observation som kanske hjälper: $q_k(x)=0$ är ekvivalent med $x^k(2-x)=1$ .

Det betyder att alla lösningar kommer att uppfylla $|x|^k|2-x|=1$ , dvs. ${|2-x|}=|x|^{-k}$ .

Så åtminstone för "stora" $k$ så betyder det att en lösning som ligger utanför enhetscirkeln (med $|x|>1$ ) kommer att behöva ligga "nära" $2$ , vilket matchar vår intuition.

Man kanske kan bygga någon slags argument baserat på detta?

Här är ett annat spår: Det finns en sats i komplex analys som heter Rouchés sats, som ibland användas för att säga något om antalet nollställen innanför en kurva $C$ i det komplexa talplanet, som kanske är tillämpbar här. Det vi vill visa är att vi har $n-1$ lösningar innanför enhetscirkeln. (Eventuellt kan det underlätta att göra ett variabelbyte $z=1/x$ så att problemet i stället blir att visa att det finns en unik lösning innanför enhetscirkeln.)

oggih skrev:
Här är ett annat spår: Det finns en sats i komplex analys som heter Rouchés sats, som ibland användas för att säga något om antalet nollställen innanför en kurva $C$ i det komplexa talplanet, som kanske är tillämpbar här. Det vi vill visa är att vi har $n-1$ lösningar innanför enhetscirkeln. (Eventuellt kan det underlätta att göra ett variabelbyte $z=1/x$ så att problemet i stället blir att visa att det finns en unik lösning innanför enhetscirkeln.)

Mycket intressanta observationer!

Gällande Rouchés sats har jag en ide. Däremot vet jag inte helt säker om den är giltig eftersom jag använder lite gränsvärden och jag aldrig sett denna sats förut.

Låt $k>1$

Vi vet att $q_k(z) = z^{k+1} - 2z^k + 1$ har samma rötter som $p_k$ , plus en extra rot vid $z=1$ . (Jag byter till $z$ eftersom allt detta är över $\mathbb C$ )

Vi delar upp $q_k(z)$ i två delar (för Rouchés sats):

$f_k = z^{k+1}+1$ och $g_k = -2z^k$

Om vi tänker oss att vår region är $|z| < r$ för något $r$ som är lite större än 1 (det viktiga nog är egentligen att $r< \frac{1+\sqrt5}2$ , eftersom det är det minsta positiva reella nollstället till p_k).

Gränsen för satsen blir då cirkeln $|z|=r$ .
På denna cirkel har vi att

$|g_k| = |-2z^k| = 2r^k$ .

Sedan måste vi visa att $2r^k> r^{k+1} + 1$ , jag hand om det senare.

I alla fall har vi då, enligt triangelolikheten:

$|g_k| =2r^k > r^{k+1} + 1 = |z^{k+1}| + |1|\geq |z^{k+1} + 1| = |f_k|$

Alltså är $|g_k| > |f_k|$ på $|z|=r$
$g_k$ har enbart roten $z=0$ på $|z| < r$ , men för Rouchés sats räknas denna rot som $k$ rötter eftersom den har multiplicitet $k$ .

Enligt Rouchés sats har vår funktion, $g_k + f_k = q_k$ , $k$ st rötter på området $|z| < r$ .
Vi vet att en av dem är $z=1$ . Eftersom detta stämmer för alla $r$ som är "lite" större än 1 borde vi nog (kan vi?) kunna ta gränsvärdet när $r \to 1$ vilket ger oss att $q_k$ har $k$ st rötter på området $|z| \leq 1$ .

Då måste vi bara visa att den enda roten med på cirkeln $|z|=1$ är $z=1$ . Efter det har vi att $q_k$ , och därmed $p_k$ , har $k-1$ st rötter på $|z| < 1$ och vi är klara.

Låt $z=e^{i\varphi}$ för något $\varphi$ .

$g_k(z)=0 \Rightarrow e^{i\varphi(k+1)}-2e^{i\varphi k} + 1 = 0$

En omskrivning med Eulers formel ger

$\cos((k+1)\varphi) -2\cos(k\varphi) + 1 + i(\sin((1+k)\varphi) - 2\sin(k\varphi))=0$

Eftersom både real och imaginärdel ska bli 0 har vi två ekvationer:

$\cos((k+1)\varphi) -2\cos(k\varphi) + 1 = 0$ (1)

$\sin((k+1)\varphi) - 2\sin(k\varphi)=0$ (2)

Omskrivning och kvadrering av den första ekvationen ger

$\cos^2((k+1)\varphi)+ 2\cos((k+1)\varphi) + 1 = 4\cos^2(k\varphi)$ (3)

Omskrivning och kvadrering av den andra ekvationen ger

$\sin^2((k+1)\varphi) =4\sin^2(k\varphi)$ (4)

Från trig-ettan på (4) har vi

$1-\cos^2((k+1)\varphi) = 4-4\cos^2(k\varphi)$

En liten omskrivning ger

$3 = 4\cos^2(k\varphi)-\cos^2((k+1)\varphi)$

(3) ger oss att HL = $2\cos((k+1)\varphi) + 1$
Substituering ger oss att
$\cos((k+1)\varphi) = 1$ , som har lösningen $\displaystyle\varphi = \frac{2\pi m}{k+1}$ , $m \in \mathbb Z$

Insättning av detta värde för $\varphi$ i (2) ger oss

$\displaystyle \sin\left((k+1)\frac{2\pi m}{k+1}\right) - 2\sin\left(k\frac{2\pi m}{k+1}\right) = 0$

Vilket innebär att

$\displaystyle\sin\left(\frac{2\pi mk}{k+1}\right) = 0$

För att detta ska stämma måste $\frac{2mk}{k+1}$ vara ett heltal.

Låt $\frac{2mk}{k+1} = b$ för något heltal $b$

Detta ger oss att $m = \frac{b(k+1)}{2k}$ , däremot är $m$ ett heltal.
Eftersom $k+1$ och $k$ är relativt prima ( $k>1$ ) måste $2k\, |\, b$ .
Alltså är $b$ en multipel av $2k$ . Då kan vi skriva $b$ som $2kc$ för något heltal c

Då är $m = c(k+1)$

Slutligen har vi då att $\varphi = \frac{2m\pi}{k+1} = 2\pi c$ . Då har vi $z = e^{i\varphi} =e^{2\pi c i} = 1$

Det sista som är kvar är då att visa att $2r^k > r^{k+1} + 1$ för alla $1<r<\frac{1+\sqrt5}2$

Med induktion:

Basfall $k=2$
$2r^2 > r^3 +1$ är ekvivalent med $r^3 - 2r^2 + 1<0$ . Detta polynom i $r$ kan faktoriseras som

$\displaystyle\left(r-1\right)\left(r-\frac{1+\sqrt5}2\right)\left(r-\frac{1-\sqrt5}{2}\right)$ .

För våra värden på $r$ är den första och tredje faktorn rätt tydligt positiv, medan den andra faktorn är negativ. Alltså kommer detta polynom alltid vara negativt över vårt intervall.

Induktionsantagande: Antag att

$2r^p > r^{p+1} + 1$ för något heltal $p \geq 2$

Eftersom $r$ är positiv är detta ekvivalent med $2r^{p+1} > r^{p+2} + r$

För induktionssteget har vi, enligt antagelsen och faktumet att $r> 1$
$2r^{p+1} > r^{p+2} + r>r^{p+2} + 1 = r^{(p+1)+1}+1$
och då stämmer påståendet för alla $1<r<\frac{1+\sqrt 5}2$ .

oggih skrev:
Ytterligare en observation som kanske hjälper: $q_k(x)=0$ är ekvivalent med $x^k(2-x)=1$ .

Det betyder att alla lösningar kommer att uppfylla $|x|^k|2-x|=1$ , dvs. ${|2-x|}=|x|^{-k}$ .

Så åtminstone för "stora" $k$ så betyder det att en lösning som ligger utanför enhetscirkeln (med $|x|>1$ ) kommer att behöva ligga "nära" $2$ , vilket matchar vår intuition.

Man kanske kan bygga någon slags argument baserat på detta?

Jag vet inte riktigt hur man skulle göra ett argument gällande detta. Om man ritar denna olikhet (exempelvis i desmos) får man denna figur:

Figuren innanför enhetscirkeln i bilden verkar vara det för alla $k>1$ , medan figuren utanför enhetscirkeln konvergerar mot 2 när $k$ ökar, vilket är förväntat.

Det är nog svårt (jag kommer inte på något just nu i alla fall) att visa att enbart en rot är utanför enhetscirkeln från denna. Eftersom absolutbeloppen är positiva kan vi kvadrera utan att ändra lösningsmängden. Om vi låter $z = x+iy$ kan likheten skrivas om till

$(x^2+y^2)^{-k} = 4-4x + x^2 + y^2$

Däremot vet jag inte om denna omskrivning är användbar..

Eller faktiskt, eftersom $x$ och $y$ är real- och imaginär-del i ett komplext tal kan vi skriva
$x= r\cos\varphi$ , $y=r\sin\varphi$

Vilket, med lite trig-ettor ger

$r^{-2k} = 4-4r\cos\varphi + r^2$

Om vi löser ut $\cos \varphi$ har vi

$\displaystyle \cos \varphi = \frac{r^2 +4-r^{-2k}}{4r}$

Och vi vet att $|\cos\varphi| \leq 1$ , där likhet bara sker när $\varphi$ är en heltalsmultipel av $\pi$ (alltså att roten är reell)

Jag måste funderar mer på detaljerna i ditt inlägg. Under tiden kan jag dela med mig av vad jag har funderat på under dagen:

Först och främst så föreslår jag att vi tar $q_k(x)=x^{k+1}-2x^k+1$ , och applicerar koordinatbytet $z=1/x$ (som flippar utsidan och insidan i enhetscirkeln), så att vi får ett nytt polynom $h_k(z)=1-2z+z^{k+1}$ . I slutändan gör det nog ingen större skillnad, men jag tycker det blir lite renare beräkningar på det gär viset.

Vi vill nu visa att $h_k(z)$ har precis ett nollställe innanför enhetscirkeln $C=\{z\in\mathbb{C}:|z|=1\}$ , vilket motsvarar att $q_k(x)$ har precis ett nollställe utanför enhetscirkeln.

Strategin som Rouchés sats föreskriver är att göra en uppdelning $h_k(z)=f(z)+g(z)$ sådan att $f(z)$ har precis en lösning innanför enhetscirkeln, och $g(z)$ är "litet" på cirkeln i bemärkelsen att $|g(z)|<|f(z)$ för $z\in C$ .

Min första gissning var att testa $f(z)=-2z$ och $g(z)=z^{k+1}+1$ . Detta fungerar nästan, eftersom $f(z)$ har en unik lösning $z=0$ (med multiplicitet 1) innanför enhetscirkeln, och enligt triangelolikheten gäller

$|g(z)|\leq |z^{k+1}|+1=2=|f(z)|$ för $z\in C$ ,

men tyvärr gäller $|g(z)|=2$ för alla lösningar till $z^{k+1}=1$ (och det finns $k+1$ sådana).

Frågan är hur illa detta är? Man kanske kan argumentera för att satsen ändå gäller om vi har strikt olikhet för "nästan alla" punkter på $C$ ?

Jag gillar idén från ditt inlägg om att välja en annan radie $r$ . Vad sägs om följande?

Låt $r\in(0,1)$ vara en radie sådan att det inte finns några lösningar till $h_k(z)=0$ med $r<|z|<1$ . Exakt vad radien är är inte viktigt, utan huvudsaken är att det alltid existerar ett sådant tal, och att vi kan välja det hur nära $1$ som helst. Det räcker nu att visa att $h_k(z)$ har en unik lösning innanför cirkeln $C_r=\{z\in\mathbb{C}:|z|=r\}$ .

Och nu tror jag Rouchés sats är tillämpbar (men det är sent på kvällen, så dubbelkolla allt ordentligt!).

Först och främst gäller det fortfarande att $f(z)$ har en unik lösning innanför $C_r$ .

Vidare så ger triangeloliklheten att för alla $z\in C_r$ så gäller $|g(z)|\leq |z^{k+1}|+|1|=r^{k+1}+1$ , vilket vi ska jämföra med $|f(z)|=2r$ .

Och om mina kvällanalysskills inte missleder mig, så kan vi garantera att $r^{k+1}+1<2r$ genom att gå tillbaka och välja $r\in (0,1)$ tillräckligt nära 1, förutsatt att $k\geq 2$ (fallet $k=1$ förstår vi redan, så det är inget problem). Se följande Geogebra-plot för intuition.

QED?

Jo, jag tror detta fungerar. $r^{k+1} + 1 < 2r$ går nog att visa med induktion utan större problem. Jag ser inga problem och Rouchés sats verkar vara tillämpbar. Snyggt!

Jag sökte runt lite, och det verkar som att den där unika positiva roten till $p_k(x)$ är ett exempel på något som kallas Pisot–Vijayaraghavan-tal. Det verkar finnas en hel del teori runt dessa, så kanske finns det något användbart kopplat till talföljderna som du studerar om du läser lite om detta.

oggih skrev:
Jag sökte runt lite, och det verkar som att den där unika positiva roten till $p_k(x)$ är ett exempel på något som kallas Pisot–Vijayaraghavan-tal. Det verkar finnas en hel del teori runt dessa, så kanske finns det något användbart kopplat till talföljderna som du studerar om du läser lite om detta.

Intressant! Ska kika vidare på det! Jag hade ingen aning om något sådant. Däremot kanske jag inte ska vara överraskad. Det finns så mycket intressanta saker som detta inom matematiken!

Svara

Visa senaste svar