Visa att Appolonius metod fungerar
Appolonius utvecklade en metod för att rita tangenten till parabeln f(x) = ax^2 (a > 0) i en punkt P. Appolonius metod kan beskrivas på följande sätt:
1. Punkten Q markeras på y-axeln så att PQ är vinkelrät mot y-axeln.
2. Punkten R markeras på y-axeln så att avståndet AR är lika med avståndet AQ, där punkten A är origo.
3. Den räta linje som går genom punkterna R och P är nu tangent till parabeln i punkten P.
Visa att Apollonius metod att konstruera tangenter fungerar för alla typer av andragradsfunktioner på formen f(x) = ax^2 där punkten P inte sammanfaller med punkten A.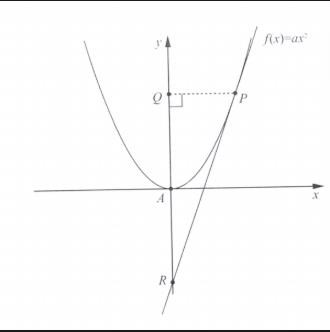
Hur löser man denna uppgift? All hjälp uppskattas.
Ett sätt att angripa detta är väl att teckna den räta linjens ekvation enligt din figur med användning av f'(x), x och -f(x).
Ge avståndet AR och AQ ett namn t.ex. "b".
f(x) = ax2 = b....x = ...
Räta linjen
k =Δy /Δx=..
f´(x) = 2ax = k
osv.



