Visa att b=-a/2
Tangentens ekvation är, y = -2x/a^3 + 3/a^2. Jag vet att man borde kunna hitta punkten b relativt enkelt med digitala verktyg, och eventuellt polynomdivision. Dock för denna uppgift ska man kunna lösa den utan några digitala verktyg. Jag kan ställa upp det till skärningen mellan funktionerna med. 1/x^2 = -2x/a^3 + 3/a^2. Vilket kan vidare utvecklas till, 0 = -2x^3/a^3 + 3x^2/a^2 - a. Då hat man en tredjegradsfunktion. Som också borde kunna omskrivas till. 0=-2x^3 + 3ax^(2) - a^3
Jag vet inte hur man kan lösa detta för hand. Eller om man kan lösa det på ett annat sätt?
Tack, för den fina genomgången samt det snabba svaret, kan man göra det utan polynomdivision? Då det inte lärts ut inom denna kurs.
Visa spoiler
Skriv ditt dolda innehåll här
Kvadrat skrev:Tack, för den fina genomgången samt det snabba svaret, kan man göra det utan polynomdivision? Då det inte lärts ut inom denna kurs.
Visa spoiler
Skriv ditt dolda innehåll här
Du skulle kunna plotta t^3-3t+2 och ana dig till var den skär x-axeln och sedan verifiera detta genom att sätta in -2 och 1. Du kommer att se att den har dubbelt nollställe för 1.
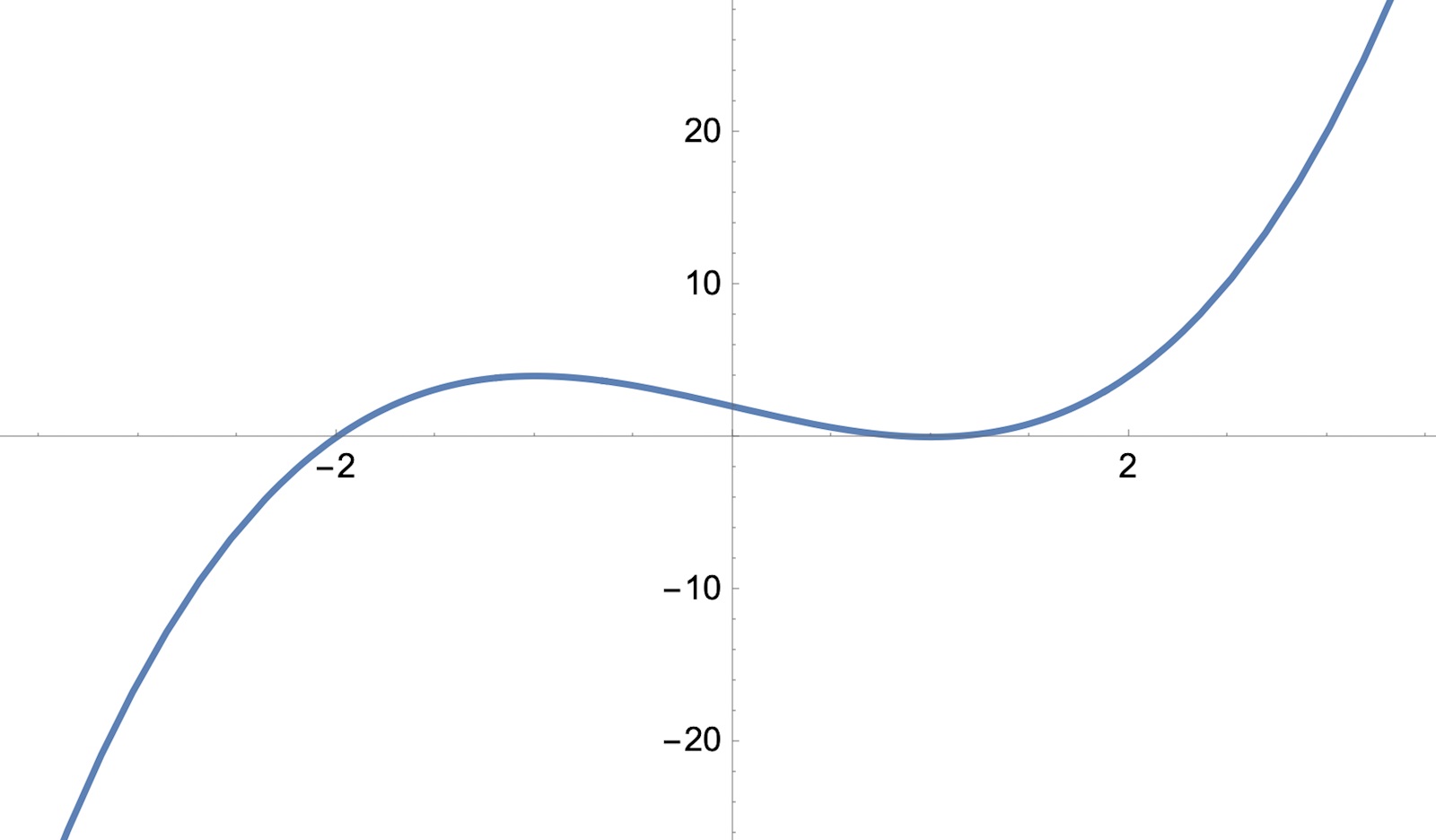
Så man kan bara mer eller mindre testa sig fram? Om man inte använder sig av varken digitala verktyg eller polynomdivision.
Kvadrat skrev:Så man kan bara mer eller mindre testa sig fram? Om man inte använder sig av varken digitala verktyg eller polynomdivision.
Ja, det tycker jag. En värdetabell på några heltal och så lite plottning. Det går fint. Så gjorde vi alla före grafritarnas tid.




