Kan jag börja med att konstruera en triangel in en cirkel med area k.
och sedan använda några trig satser ?
Ett alternativ (hämtat från nätet);
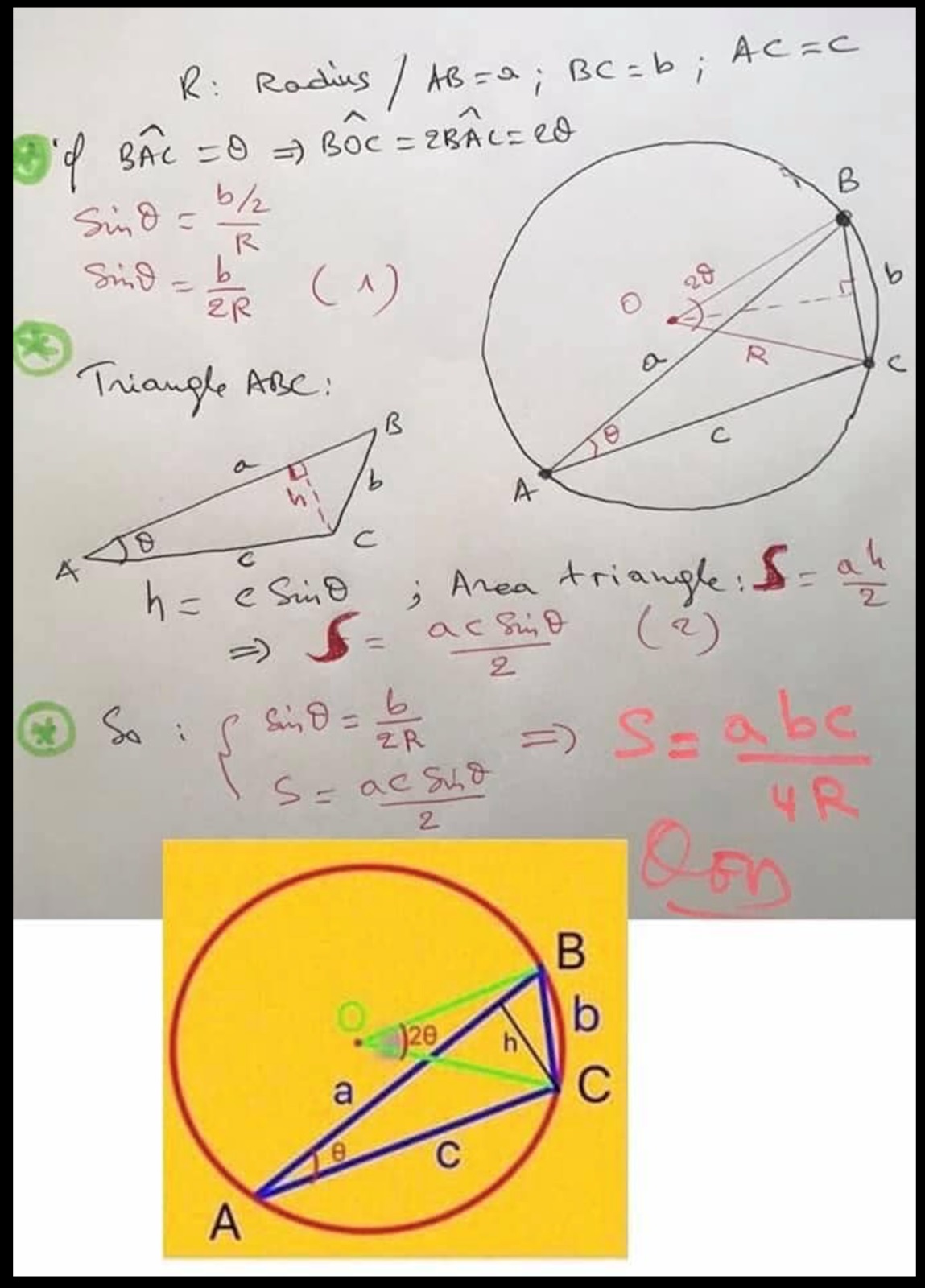
Jag sökte på det här problemet och det verkar vara rätt så känt
Hittade en till
Trinity du får gärna säga vilken dessa du tyckte löste frågan bäst
En av mina fantastiska gymnasielärare löste essentiellt detta problem (följdsats) på en lektion som jag faktiskt har en bild ifrån (bifogad) Sats 3 på tavlan tillsammans med areasatsen implicerar direkt den sökta likheten:
Sats 3 på tavlan tillsammans med areasatsen implicerar direkt den sökta likheten:
Vi har enligt areasatsen. Sedan ger Sats 3 att . Insättning i uttrycket från areasatsen medför svaret.
Beviset för Sats 3 följer från den nedre triangeln. Stegen går ungefär såhär:
Rita en inskriven triangel och kalla mittpunkten i triangeln för . Drag diametern genom och och kalla den andra skärningspunkten för . Randvinkelsatsen (i bilden nämns speciallfallet Thales sats) ger att .
Randvinkelsatsen ger också att , då båda är randvinklar till samma medelpunktsvinkel. Därmed har de samma sinusvärden, dvs . Då rätvinklig enligt tidigare diskussion är
Fallen för och följer analogt.
var det här i ma 4 ?
AlexMu skrev:En av mina fantastiska gymnasielärare löste essentiellt detta problem (följdsats) på en lektion som jag faktiskt har en bild ifrån (bifogad)
Sats 3 på tavlan tillsammans med areasatsen implicerar direkt den sökta likheten:
Vi har enligt areasatsen. Sedan ger Sats 3 att . Insättning i uttrycket från areasatsen medför svaret.
Beviset för Sats 3 följer från den nedre triangeln. Stegen går ungefär såhär:
Rita en inskriven triangel och kalla mittpunkten i triangeln för . Drag diametern genom och och kalla den andra skärningspunkten för . Randvinkelsatsen (i bilden nämns speciallfallet Thales sats) ger att .
Randvinkelsatsen ger också att , då båda är randvinklar till samma medelpunktsvinkel. Därmed har de samma sinusvärden, dvs . Då rätvinklig enligt tidigare diskussion är
Fallen för och följer analogt.
jag är trött... vad är k i bilden?
IMO rörig tavelteknik men kanske underlättas av det talande språket...
Arup skrev:Trinity du får gärna säga vilken dessa du tyckte löste frågan bäst
#2, men det är samma som Math Booster. Sedan kan man alltid diskutera vilka "verktyg" man får använda, men det tycker jag är en meningslös diskussion inom matematiken. Använd det du kan. Kunskap är aldrig en börda.
Trinity2 skrev:jag är trött... vad är k i bilden?
IMO rörig tavelteknik men kanske underlättas av det talande språket...
finns ej i bilden jag bifogade, men ska vara arean av enligt bilden i #1 (det låter från meningen att det är cirkeln har area , men i så fall stämmer inte den givna formeln, måste vara triangelns area).
Jag tyckte alltid dessa lektioner var riktigt bra genomförda. Det var alltid tydligt och trevligt!
Arup skrev:var det här i ma 4 ?
Nej, det var i en matte spec kurs i problemlösning (innefattade lite talteori, kombinatorik, geometri, mm). Just denna lektion handlade om inskrivna och omskrivna trianglar.
AlexMu skrev:Trinity2 skrev:jag är trött... vad är k i bilden?
IMO rörig tavelteknik men kanske underlättas av det talande språket...
finns ej i bilden jag bifogade, men ska vara arean av enligt bilden i #1 (det låter från meningen att det är cirkeln har area , men i så fall stämmer inte den givna formeln, måste vara triangelns area).
Jag tyckte alltid dessa lektioner var riktigt bra genomförda. Det var alltid tydligt och trevligt!
Tvivlar inte på att det finns bra lärare och det är inte alltid ord kan förmedla en bra presentation så bilder kan vara missvisande för helheten. Jag tyckte bara det såg rörigt ut på bilden. Det var lite av Post-It-karraktär. Hur många varv krävs det för att rita en cirkel ? :)
https://www.youtube.com/watch?v=eAhfZUZiwSE
Min gymn.lärare i matematik var nästan lika skicklig. Första gången man såg det tappade man hakan. Jag har aldrig lyckats själv. Jag anv. passare... mes som jag är...
AlexMu skrev:Arup skrev:var det här i ma 4 ?
Nej, det var i en matte spec kurs i problemlösning (innefattade lite talteori, kombinatorik, geometri, mm). Just denna lektion handlade om inskrivna och omskrivna trianglar.
Jag tror Torbjörn Tambour höll en geometrikurs för ett par år sedan vid SU med lite mera "klassis geometri". Tror hans kompendium finns på nätet någonstans. Kommer ej ihåg var dock. Det innehöll även lite kluriga övningsuppgifter vill jag minnas. Dock inget facit IIRC så man är lite ovetandes om sitt resultat i vissa uppgifter...