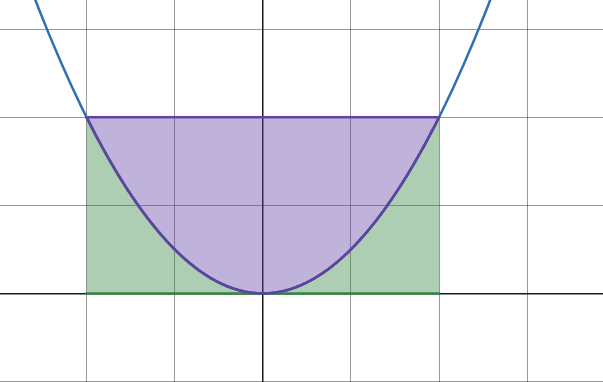
Visa att det skuggade området är 2/3 (Matematik/Matte 3/Integraler)

Så här tänker jag

Hej, det du har beräknat är arean mellan parabeln och x-axeln.

Du behöver även visa att denna area är 1/3 av rektangelns area.

(En annan kommentar är att du har skrivit F(-a) som -a³/3 istället för (-a)³/3)

Är inte det samma sak ?

Arup skrev:
Är inte det samma sak ?

Du har räknat det gröna området. Du söker det lila.

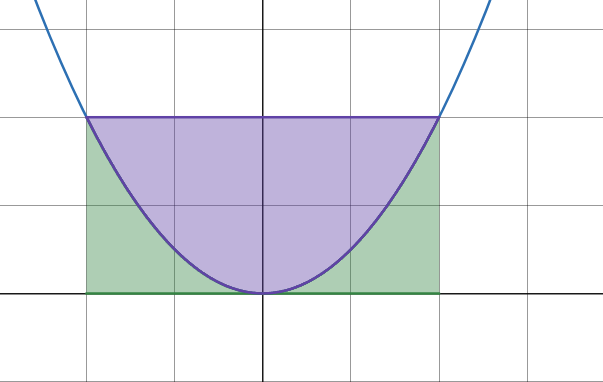
Man skulle väl kunna räkna integralen över funktionen $a^2-x^2$ ?

Arup skrev:
Är inte det samma sak ?

Nej, men du får gärna beskriva hur du tänker så vi kan hjälpa dig att hitta var det går fel.

Yngve skrev:
Arup skrev:
Är inte det samma sak ?

Nej, men du får gärna beskriva hur du tänker så vi kan hjälpa dig att hitta var det går fel.

Ja mena får inte jag samma svar på funktionen F(-a) som $- \frac{a^{3}}{3}$ som $\frac{{(- a)}^{3}}{3}$ ?

Arup skrev:

Ja mena får inte jag samma svar på funktionen F(-a) som $- \frac{a^{3}}{3}$ som $\frac{{(- a)}^{3}}{3}$ ?

Jo, i det här fallet är det så, eftersom exponenten är udda.

Men om funktionen istället hade varit F(x) = x² så skulle du fått olika svar.

Jag har gjort ett nytt försök

Om du istället tar delen / hela (alltså skuggan / rektangeln) så får du 2/3 som uppgiften ber dig visa. Som du ställt upp på sista raden så är uttrycket =3 (och inte 1/3).

sictransit skrev:
Om du istället tar delen / hela (alltså skuggan / rektangeln) så får du 2/3 som uppgiften ber dig visa. Som du ställt upp på sista raden så är uttrycket =3 (och inte 1/3).

Hur menar du ?

De här är mitt nya försök, men jag får dessvärre fel

Integralen ger dig inte arean på det skuggade området

AlexMu skrev:
Integralen ger dig inte arean på det skuggade området

vad ger den då ?

AlexMu skrev:
Du har räknat det gröna området. Du söker det lila.

Detta inlägg gäller fortfarande!

blir det då $1 - \frac{1}{3}$

Ja.

========

Du kan göra på olika sätt.

Ett sätt är att räkna ut arean av det lila området A_lila direkt med en enda integralberäkning.

Då kan du använda att arean av området mellan två funktionsgrafer f(x) och g(x) från x₁till x₂ kan beräknas som integralen från x₁ till x₂ av ("den övre funktionen" minus "den undre funktionen").

Detta beskrivs närmare här.

Om då g(x) $\geq$ f(x) I hela intervallet så blir arean $A_{lila}=\int_{x_1}^{x_2}(g(x)-f(x))\operatorname dx$

Tillämpat i detta fall så har du att

x₁ = -a
x₂ = a
f(x) = x² (den "undre funktionen", vars graf är parabeln y = x²)
g(x) = a² (den "övre funktionen", vars graf ör den horisontella linjen y = a²)

Vilket ger dig $A_{lila}=\int_{-a}^{a}(a^2-x^2)\operatorname dx$

Och sedan beräkna det som efterfrågas, nämligen A_lila/A_rektangel

========

Ett annat sätt är att beräkna arean av det gröna området A_grön och sedan använda att arean av det lila området A_lila är lika med arean av rektangeln minus arean av det gröna området, dvs A_lila = A_rektangel- A_grön

Och sedan beräkna det som efterfrågas, nämligen A_lila/A_rektangel

========

Ett tredje sätt är att beräkna hur stor andel som det gröna området utgör av rektangeln och sedan resonera sig fram till det du skriver, nämligen att det som efterfrågas är 1-A_grön/A_rektangel

Sen finns det såklart förenklingar att göra, t.ex. att se att det pga symmetri räcker att beräkna areorna och andelarna av områdena i första kvadranten, dvs det räcker att integrera från x = 0 till x = a.

Yngve är det så här du menade i första stycket ?

jag undrar varför får jag 1/3 och inte 2/3 ?

Du får fel svar när du integrerar. Jag tar det steg för steg.

$\int_{- a}^{a} (a^{2} - x^{2}) d x = {[a^{2} x - \frac{x^{3}}{3}]}_{- a}^{a} = (a^{2} \times a - \frac{a^{3}}{3}) - (a^{2} \times - a - \frac{{(- a)}^{3}}{3}) = (a^{3} - \frac{a^{3}}{3}) - (- a^{3} - \frac{- a^{3}}{3}) = a^{3} - \frac{a^{3}}{3} - (- a^{3} + \frac{a^{3}}{3}) = a^{3} - \frac{a^{3}}{3} + a^{3} - \frac{a^{3}}{3} = 2 a^{3} - \frac{2 a^{3}}{3} = \frac{4 a^{3}}{3}$

$\frac{\frac{4 a^{3}}{3}}{2 a^{3}} = \frac{4 a^{3}}{2 a^{3} \times 3} = \frac{4}{6} = \frac{2}{3}$

Blir inte integralen av a^2 =a^3/3 ?

Arup skrev:
Blir inte integralen av a^2 =a^3/3 ?

$\int_{}^{} a^{2} d x = a^{2} x + C$

$\int_{}^{} a^{2} d a = \frac{a^{3}}{3} + C$

Så varför blir det inte a^3 /3 ?

Om du integrerar över x, så är a en konstant.

$\int 42 d x = 42 x + C$

Du har säkert löst något i den här stilen tidigare:

$\int_{0}^{1} 4 x d x = {[4 \frac{x^{2}}{2}]}_{0}^{1} = (4 \frac{1^{2}}{2}) - (0) = 2$

Fyran är en konstant och det skulle lika gärna kunna stå ett a där.

Ok nu tror jag förstår

Jag har en fråga behöver du inte integrera a^2 ?

Arup skrev:
Jag har en fråga behöver du inte integrera a^2 ?

Det är så många olika uttryck och integraler här så det är svårt att veta vilket a² du menar.

Kan du skriva på ett papper den integral du undrar över och ladda upp en bild?

Arup skrev:
Jag har en fråga behöver du inte integrera a^2 ?

Jo, det gör jag ju:

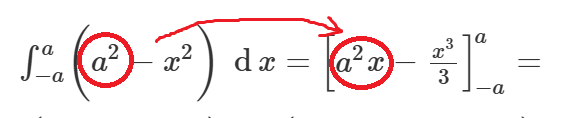
Om det inte är det du menar, gör som Yngve föreslår och ladda upp en bild på det du funderar över.

Det var den jag mena

Arup skrev:
Det var den jag mena

OK. Undrar du alltså varför den primitiva funktionen av den termen blir a²x istället för a³/3?

ja

OK.

Vi tar ett par andra exempel för att förtydliga.

Är du med på att

en primitiv funktion till konstanten 3 är 3x, eftersom x-derivatan av 3x är 3?
en primitiv funktion till konstanten b är bx, eftersom x-derivatan av bx är b?
en primitiv funktion till konstanten b² är b²x, eftersom x-derivatan av b²x är b²?

ja

Bra.

Är du då även med på att en primitiv funktion till konstanten a² är a²x, eftersom x-derivatan av a²x är a²?