Visa att diskriminanten är lika
Hej! Jag har kört fast på följande fråga, jag har verkligen ingen tanke om hur jag kan följa eller något, så det är en lite dålig tråd jag postar nu, men jag hade verkligen behövt lite input med ideér kring hur jag kan komma med ett bevis till det. Jag vet att jag egentlige vill kasta om uttrycket som står i abc-form till något som liknar på, men då gäller att x2 står utan koefficient och det gör det inte just nu, men jag kan väl heller inte dividera med a, för om a vore 0 (då skulle i och för sig hela x2 försvinna), men det skulle bli som att dividera med 0, för just nu vet vi ju inte a. Såvida man inge gör antagandet att a>0

Tack på förhand :)
Eftersom det är en andragradsekvation, kan vi tryggt utgå från att a ≠ 0 .
Ok, tack för ditt svar!
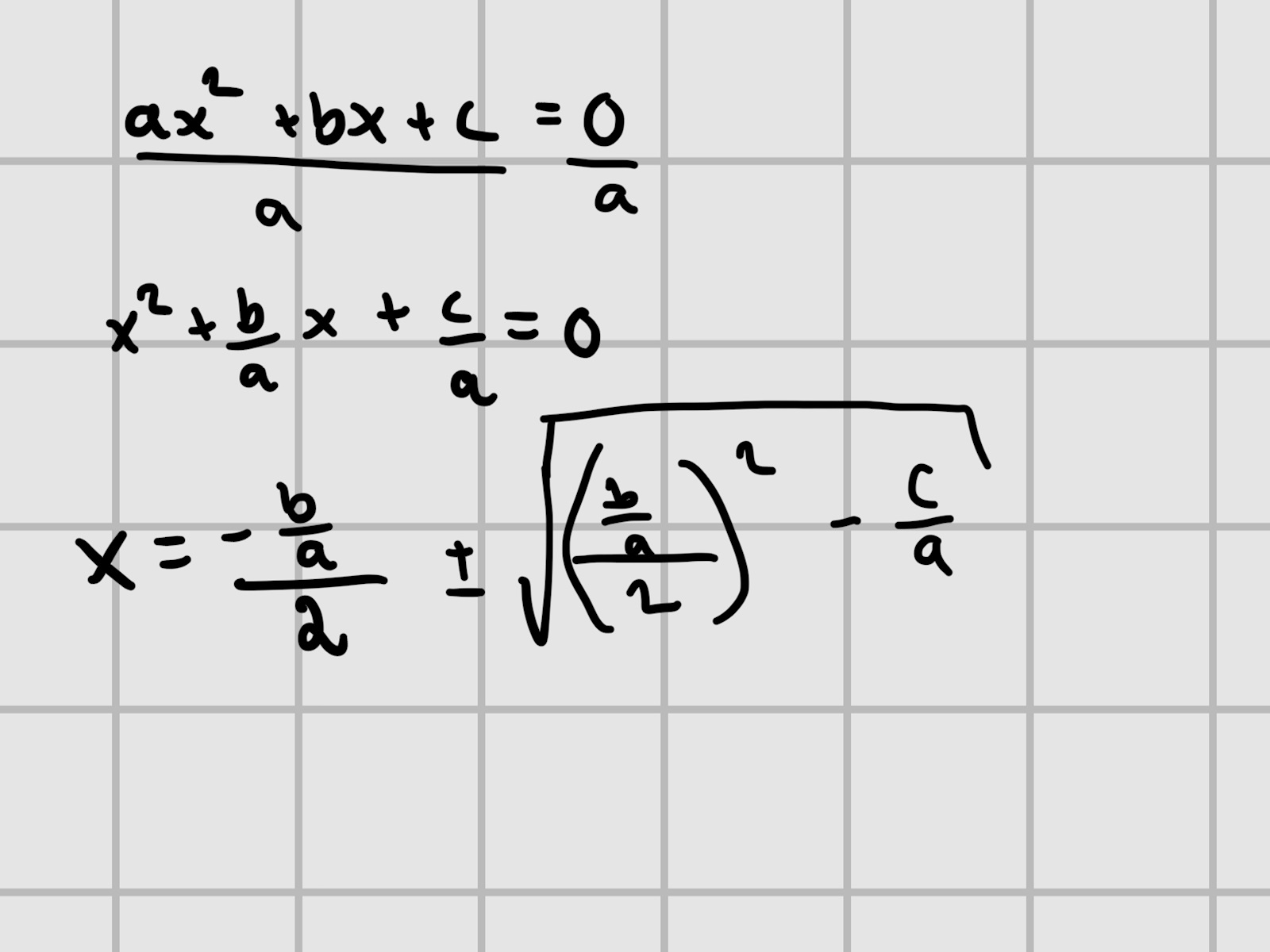
Så långt har jag kommit nu. Är jag på rätt väg eller har jag gjort något fel än så länge? Min tanke är att ta ut diskriminanten och förenkla den så långt som möjligt. Men jag inser nu att det inte riktigt var vad de frågade efter och de ville att man först skulle skriva om det som pq istället. Kan p=b/a och q=c/a i så fall? Då vet man att skulle man stoppa in de bråkvärdena istället för p och q så kommer man hamna där jag är nu.
Det ser bra ut.
Det återstår att visa att den nya diskriminanten, dvs uttrycket under rotmärket,
har samma tecken som den gamla, dvs samma tecken som b2 - 4ac.
Se uppgiftstexten.
Du ska alltså inte visa att diskriminanterna är lika (för så behöver det inte vara)
utan bara att de alltid har samma tecken.
När den ena är positiv så är den andra också positiv
När den ena är negativ så är den andra också negativ
När den ena är noll så är den andra också noll
Tips: Om man multiplicerar ett uttryck med en positiv konstant,
så har det nya uttrycket alltid samma tecken som det gamla


