Visa att en punkt tillhör en triangel
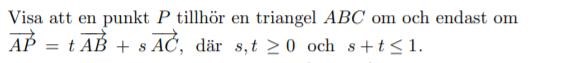
Hej, jag ska visa ovanstående och började med att försöka rita en bild för att se om jag kunde se något samband eller något som stack ut, min bild säger inte så mycket så det kanske inte är så chockande att jag inte blev något klokare av det. 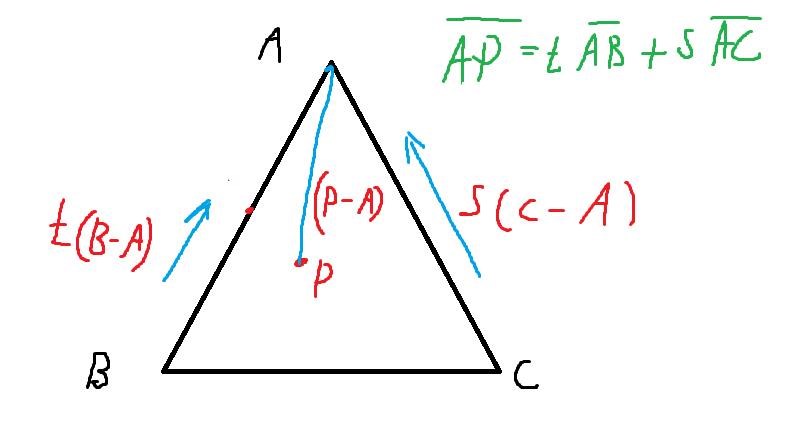
Sätt punkten A i origo i ett (inte nödvändigtvis vinkelrätt) kvadratsystem, där de båda koordinataxlarna är AB respektive AC. Vilka koordinater har punkten P i detta koordinatsystem?
Hej jag har en förklaring. Tar lite tid innan den är uppe eftersom den har figur och så.
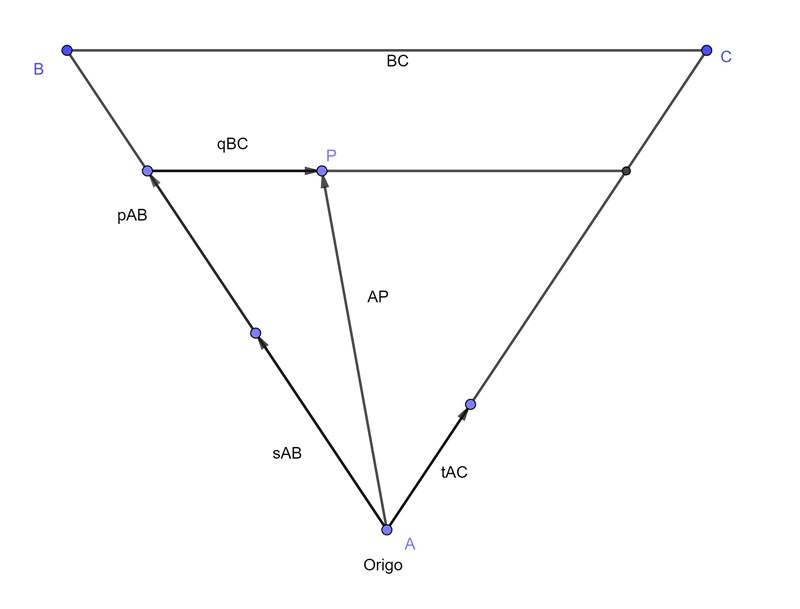
Rör det sig om en 1p uppgift så kanske det räcker med att bara utifrån figuren konstatera att s+t<1 . Och så är uppgiften löst. Annars kan man använda algebra som jag gjort nedan.
AP representerar vektorn som hör till en godtycklig punkt i triangeln. AP uttrycks med vektorerna AB och AC. Då en specifik AP väljs får s och t specifika värden, tex 0.25 och 0.3. Varken s eller t kan vara större än 1 eftersom då rör vi oss utanför triangeln. S eller t kan däremot vara 0 för då rör man sig längs ett av triangelns kateter.
Låt pAB representera en godtycklig punkt på sträckan AB. AB anger att vi är på AB kateten medan p anger exakt var. Vandrar man sen från den här punken med riktningen BC så kan vi hamna i punkten P. Skillnaden är att istället för att använda oss av AB och AC som tidigare så gör vi det genom att använda riktningarna AB och BC istället. Samma begränsningar gäller för p och q som gäller för s och t, dvs 0<p,q<1. Det är viktigt här att poängtera att p och s är inte samma tal. Geometrin hade inte gått ihop om så var fallet.
Vi har alltså 2 sätt att utrycka vektorn AP på:
AP=sAB+tAC
AP=pAB+qBC
vilket leder till en vektorekvation:
sAB+tAC=pAB+qBC
Eftersom det alltid gäller att AB-AC=CB (alt AB=AC+CB) blir det
sAB+tAC=pAB+q(AB-AC)
arrangerar AB och AC på varsin sida
tAC+qAC=pAB+qAB-sAB
AC(t+q)=(p+q-s)AB
Eftersom AC och AB inte är parallella (annars hade det inte funnits ngn triangel) så vet vi även att ingen numerisk faktor kan användas för att konvertera mellan vektorerna AC och AB. Den enda möjligheten är då att paranteserna båda är lika med 0.
t+q=0
p+q-s=0
->
t+q=p+q-s
t+s=p
Vi vet sedan tidigare att vilket i sin tur medför att .
oneplusone2 skrev:
Rör det sig om en 1p uppgift så kanske det räcker med att bara utifrån figuren konstatera att s+t<1 . Och så är uppgiften löst. Annars kan man använda algebra som jag gjort nedan.
AP representerar vektorn som hör till en godtycklig punkt i triangeln. AP uttrycks med vektorerna AB och AC. Då en specifik AP väljs får s och t specifika värden, tex 0.25 och 0.3. Varken s eller t kan vara större än 1 eftersom då rör vi oss utanför triangeln. S eller t kan däremot vara 0 för då rör man sig längs ett av triangelns kateter.
Låt pAB representera en godtycklig punkt på sträckan AB. AB anger att vi är på AB kateten medan p anger exakt var. Vandrar man sen från den här punken med riktningen BC så kan vi hamna i punkten P. Skillnaden är att istället för att använda oss av AB och AC som tidigare så gör vi det genom att använda riktningarna AB och BC istället. Samma begränsningar gäller för p och q som gäller för s och t, dvs 0<p,q<1. Det är viktigt här att poängtera att p och s är inte samma tal. Geometrin hade inte gått ihop om så var fallet.
Vi har alltså 2 sätt att utrycka vektorn AP på:
AP=sAB+tAC
AP=pAB+qBCvilket leder till en vektorekvation:
sAB+tAC=pAB+qBC
Eftersom det alltid gäller att AB-AC=CB (alt AB=AC+CB) blir det
sAB+tAC=pAB+q(AB-AC)
arrangerar AB och AC på varsin sida
tAC+qAC=pAB+qAB-sAB
AC(t+q)=(p+q-s)AB
Eftersom AC och AB inte är parallella (annars hade det inte funnits ngn triangel) så vet vi även att ingen numerisk faktor kan användas för att konvertera mellan vektorerna AC och AB. Den enda möjligheten är då att paranteserna båda är lika med 0.
t+q=0
p+q-s=0->
t+q=p+q-s
t+s=pVi vet sedan tidigare att vilket i sin tur medför att .
Oj, detta var super fint och lätt att följa! Min triangel som jag ritade hade endast med sAC och tAB samt A,b,c ( följde tipset jag fick av Smaragdalena och lade A som origo) och jag kunde inte se ett sett att motivera det åt andra hållet algebraiskt vilket du väldigt fint har visat ovan.
Tack så hemskt mycket tiill er båda! :)