Visa att ett uttryck kan skrivas som
Hej!
Visa att a×n! + a(n+1)! Kan skrivas som a×n!(n+2).
Hur visar man det?
Skriv om .
Därefter kan du bryta ut gemensamma faktorer och . Efter utbrytningen får du kvar.
Okej prövar imorgon.. Tack för det
Nej, jag förstår inte

Kollade facit då det är för svårt, jag hade ej grejat det på egen hand.
Tack för hjälpen.
Tänk dig att du har och bryter ut . Får du verkligen ?
- Nej, det blir
(Istället för så står det i denna uppgift.)
Såhär blir det då för mig.

Du menar såhär tror jag..
Det här ämnet är helt otroligt svårt för mig, jag begriper det inte. Ansträngning är näst intill oväsentlig. Det krävs naturlig fallenhet för att bli ok på det här, så är det bara. Tråkigt. Ändå kan man inte sluta hålla på med det i alla fall, märkligt.

Visa spoiler
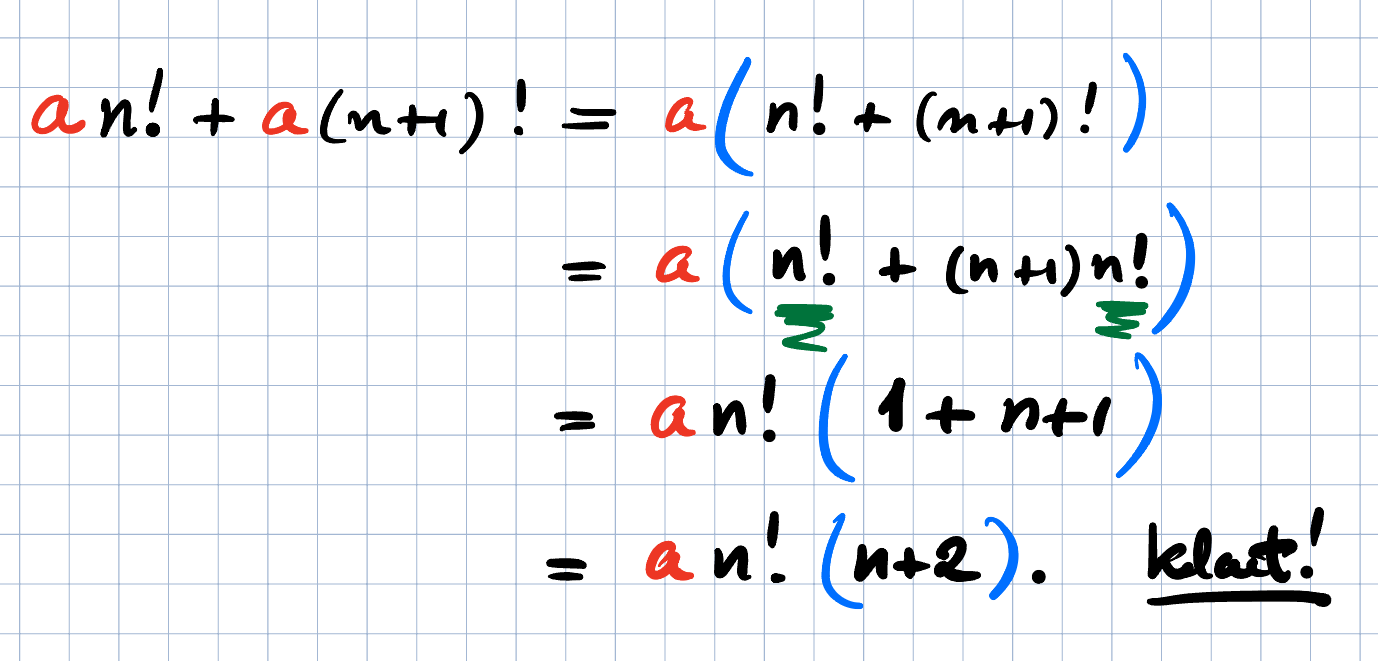
Tack!


