Visa att eulers ekvation mha indexnotation
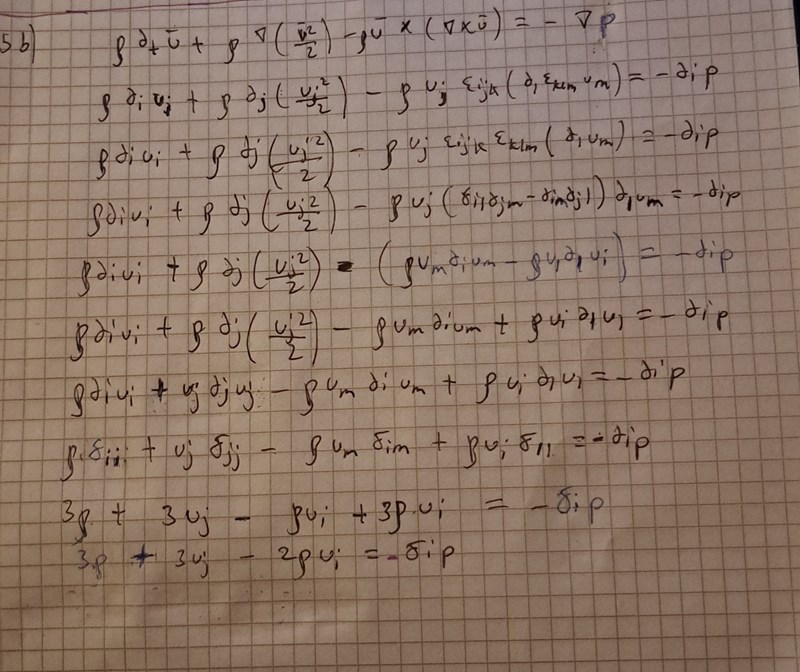

Hej!
Såhär långt kom jag i b) uppgiften , men det verkar inte bli något att HL=VL liknar varandra.
Jag skulle fokusera på att försöka visa att
.
PATENTERAMERA skrev:Jag skulle fokusera på att försöka visa att
.
Varför då? Varför kan man inte skriva högerledet som detta nedan och utnyttja index på den? Att visa VL är lika med HL som jag gjort är väl inte fel heller? Hur vet man vad man som är enkelt att fokusera på eller inte? Jag tänkte fortsätta på mitt sätt och se vart det leder till så att jag inte suddar allt jag gjort i #1.
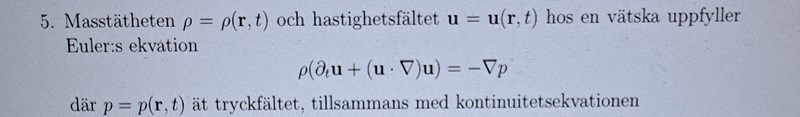
Du kan se direkt på sista raden att något gått väldigt fel.
Första termen saknar index - en skalär.
Andra termen har index j - en vektor.
Tredje termen har index i - en vektor.
I en tensorekvation så måste alla termer ha samma fria index annars blir det nonsens.
PATENTERAMERA skrev:Du kan se direkt på sista raden att något gått väldigt fel.
Första termen saknar index - en skalär.
Andra termen har index j - en vektor.
Tredje termen har index i - en vektor.
I en tensorekvation så måste alla termer ha samma fria index annars blir det nonsens.
Nu förstår jag inte riktigt. Första termen skrev jag av uppgiften bara. Där är det ingen index. De andra sakerna du nämner förstår jag inte varför de ska vara som du säger. Jag tycker vi borde gå igenom varje term steg för steg och korrigera detta för att få ett förståeligt resultat och förklaring till varför vi ska korrigera alla termer. Jag visste inte ens om det här slutsvaret var varken rätt eller fel , förutom när du själv skrev att det inte var rätt, hur ser man om man gjort rätt ? Jag försökte översätta till vektornation och fick ej att likna det som -delta p
Om vi sätter rho lika med 1 medan vi räknar så kan ekvationen skrivas
.
Ett fritt index i i varje term. En vektorekvation.
PATENTERAMERA skrev:Om vi sätter rho lika med 1 medan vi räknar så kan ekvationen skrivas
.
Ett fritt index i i varje term. En vektorekvation.
Var är fritt index i varje term? Jag är ej med riktigt. Kan man inte skriva divi? Vad är iden med fritt index?
Ett fritt index är ett index som bara förekommer en gång i en term. Här det i som är det fria indexet. Alla andra index förekommer två gånger; de kallas dummyindex och implicerar summation.
, här är i ett dummyindex och uttrycket representerar en skalär storhet - inget fritt index alls.
PATENTERAMERA skrev:Ett fritt index är ett index som bara förekommer en gång i en term. Här det i som är det fria indexet. Alla andra index förekommer två gånger; de kallas dummyindex och implicerar summation.
, här är i ett dummyindex och uttrycket representerar en skalär storhet - inget fritt index alls.
Ok jag förstår. Så eftersom vi vill att hela uttrycket hos VL ska motsvara en vektor dvs nabla P så måste vi ha ett fritt index på alla termer hos VL? Men varför är det inte ok med diui+di(ujuj)?
di(ujuj) är OK, j:et indikerar ju summation så du kan använda vilken bokstav som helst som dummyindex. , blir samma.
Återigen så blir diui en skalär - se #8. Eftersom i skall vara det fria indexet så skall du inte använda det som dummyindex.
PATENTERAMERA skrev:di(ujuj) är OK, j:et indikerar ju summation så du kan använda vilken bokstav som helst som dummyindex. , blir samma.
Återigen så blir diui en skalär - se #8. Eftersom i skall vara det fria indexet så skall du inte använda det som dummyindex.
OK så det är bättre med diuk istället för diui?
Det beror på vad du är ute efter. Båda är möjliga rent formellt. Den första representerar en andra ordningens tensor (två fria index) och den andra representerar en skalär (inget fritt index).
PATENTERAMERA skrev:Det beror på vad du är ute efter. Båda är möjliga rent formellt. Den första representerar en andra ordningens tensor (två fria index) och den andra representerar en skalär (inget fritt index).
Vi vill ju ha ett fritt index på vardera term hos VL och då är det bra att vi får diu bara och inte de jag skrev i #11
Visa vad du menar. Hänger inte med.
PATENTERAMERA skrev:Visa vad du menar. Hänger inte med.
Allt har ett fritt index precis som du sa.
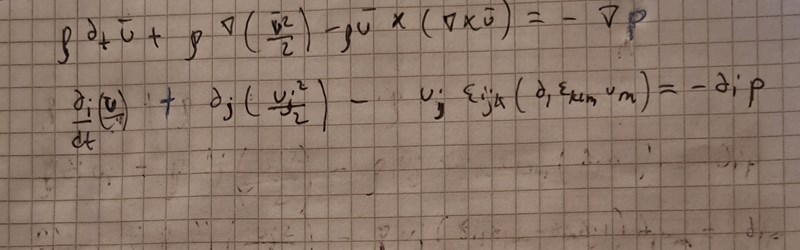
Nja.
PATENTERAMERA skrev:Nja.
Ja jag korrigerade detta. Se bild nedan. Såhär långt kom jag: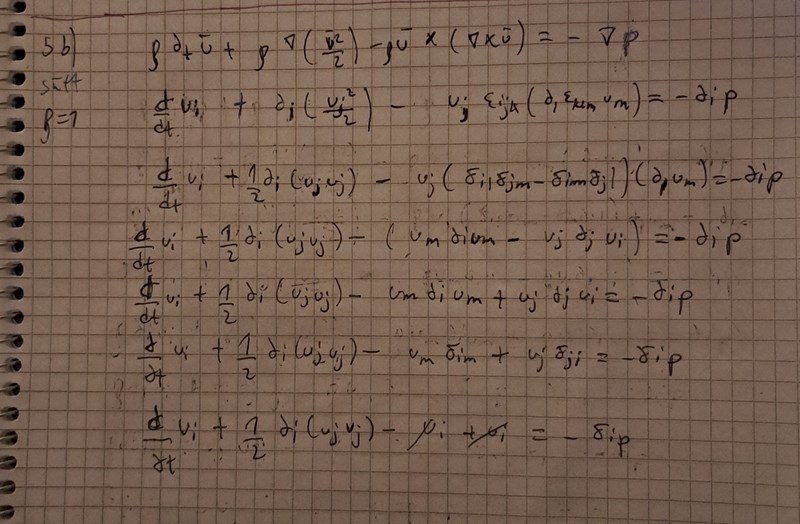
 Det är inte korrekt att tex .
Det är inte korrekt att tex .
Satsa istället på att utveckla den term som jag ringat in.
PATENTERAMERA skrev:
Det är inte korrekt att tex .
Satsa istället på att utveckla den term som jag ringat in.
Varför är det inte korrekt? Och när gäller detta och när gäller det inte?
Varför skulle det vara korrekt?
Jag tror du blandar ihop med .
PATENTERAMERA skrev:Varför skulle det vara korrekt?
Jag tror du blandar ihop med .
Därför att &ij=djri gäller men de jag skrev gäller inte. Jag förstår inte varför, det är inte så att allt är trivialt för mig. Det där du skrev är jag inte heller bekant med , så den får du gärna förklara också. Utöver detta får du även förklara varför jag ska utveckla 1/2di(ujuj) termen.
ri är ju inte samma sak som ui.
PATENTERAMERA skrev:ri är ju inte samma sak som ui.
nä ok. håller med, men varför gäller det inte då? svara gärna på mina andra frågor också.
Tänk efter vad det betyder.
Sätt in specifika värden på indexen.
Men inget säger väl att alltid måste bli 1 eller att alltid måste bli 0 för alla möjliga hastighetsfält .
Du kommer förhoppningsvis se fördelen med utvecklingen när du gör den.
PATENTERAMERA skrev:Tänk efter vad det betyder.
Sätt in specifika värden på indexen.
Men inget säger väl att alltid måste bli 1 eller att alltid måste bli 0 för alla möjliga hastighetsfält .
Jaha ok. Men varför är dx/dy=0?
Det tror jag du vet. Du har en funktion som bara beror av x, vad blir dess derivata map y?
PATENTERAMERA skrev:Det tror jag du vet. Du har en funktion som bara beror av x, vad blir dess derivata map y?
0 såklart
Såhär långt har jag kommit.
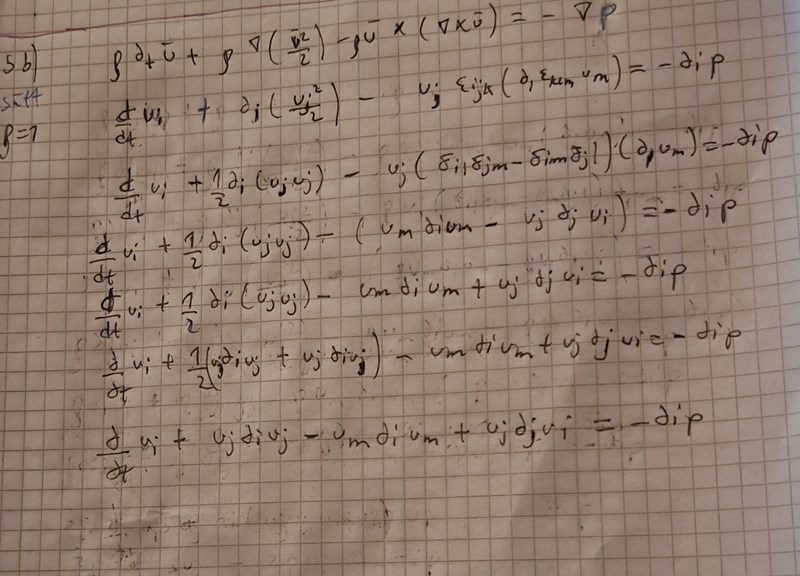
 Vad blir det inringade. Tänk på att du kan byta namn på ett dummyindex. Tex kan du döpa om m till j.
Vad blir det inringade. Tänk på att du kan byta namn på ett dummyindex. Tex kan du döpa om m till j.
PATENTERAMERA skrev:
Vad blir det inringade. Tänk på att du kan byta namn på ett dummyindex. Tex kan du döpa om m till j.
Vad är syftet med att byta namn på dummyindex då till j eller m? Jag ser inte var vi är på väg.
Gör det, och jämför med termen innan.
PATENTERAMERA skrev:
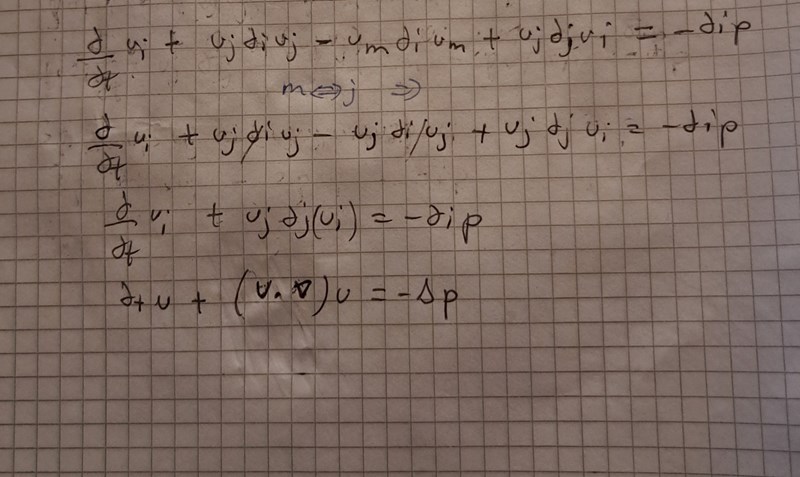
Så vad var syftet med index skifte från m till j?
Termerna tar ut varandara.
Så du är klar nu. Om du sätter in rho igen på sista raden så ser du att den är pricis det du skulle visa.
PATENTERAMERA skrev:Termerna tar ut varandara.
Så du är klar nu. Om du sätter in rho igen på sista raden så ser du att den är pricis det du sklulle visa.
Ja ok då är jag med.



