Visa att fältet är konservativt och bestäm dess potential


Hej!
Facit säger att det finns en potential men jag får tyvärr inte samma svar och det får mig att undra hur man ska se fältet som står i frågan speciellt termen med parentesen. Jag tolkar som en multiplikation mellan första termen och termen i parentesen.
Ett konservativt vektorfält har curl = 0. För ett tvådimensionellt vektorfält så innebär det i praktiken att
Så vad du bör bestämma är de här uttrycken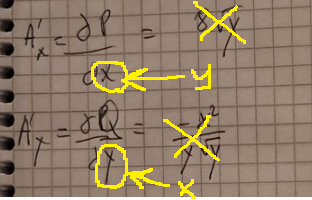
Lasse Vegas skrev:Så vad du bör bestämma är de här uttrycken
Hur menar du med att bestämma de här uttrycken?
Du deriverar den första map y och den andra map x, tvärtemot hur du gjorde först.
Micimacko skrev:Du deriverar den första map y och den andra map x, tvärtemot hur du gjorde först.
Aha varför gör man så ? Eller ska man bara inte skriva upp som de är utan att derivera? Man deriverar väl senare efter man integrerat map på en annan variabel
Jag vet inte om det rekommenderas, men jag hade nog bara slängt på en z-del som är 0 och räknat som du har gjort hittills. Någon annan kan säkert förklara varför bättre, det här var väldigt länge sedan jag läste.
Slängde ihop det lite halvsnabbt i paint så förlåt om något ser otydligt ut.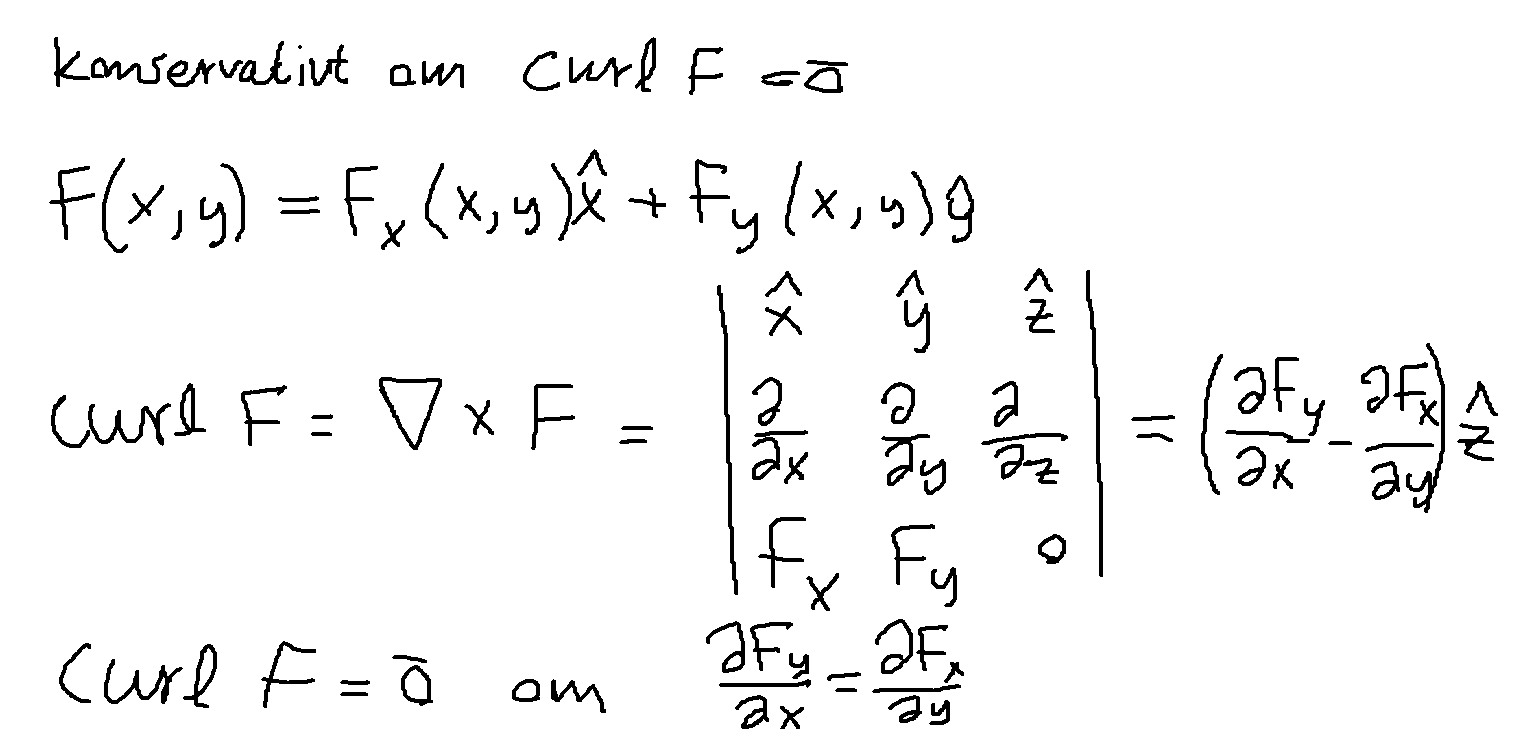 Man ska alltså beräkna dFy/dx och dFx/dy och se om de är lika med varandra. Om de är samma så är fältet konservativt.
Man ska alltså beräkna dFy/dx och dFx/dy och se om de är lika med varandra. Om de är samma så är fältet konservativt.
Lasse Vegas skrev:Slängde ihop det lite halvsnabbt i paint så förlåt om något ser otydligt ut.
Man ska alltså beräkna dFy/dx och dFx/dy och se om de är lika med varandra. Om de är samma så är fältet konservativt.
Ser ut om rotationen av ett vektorfältet. Så man ska derivera funktionens y komponent map x och sätta den lika med den deriverade funktionens x komponent map på y?
Man sätter de inte nödvändigtvis lika med varandra, utan man beräknar båda var för sig och kollar sedab om de är samma. dFy/dx = dFx/dy är alltså ett villkor som måste vara uppfyllt för att fältet ska vara konservativt.
Lasse Vegas skrev:Man sätter de inte nödvändigtvis lika med varandra, utan man beräknar båda var för sig och kollar sedab om de är samma. dFy/dx = dFx/dy är alltså ett villkor som måste vara uppfyllt för att fältet ska vara konservativt.
Ja okej jag förstår! Tack! Sen är det bara att hitta potential som vanligt.