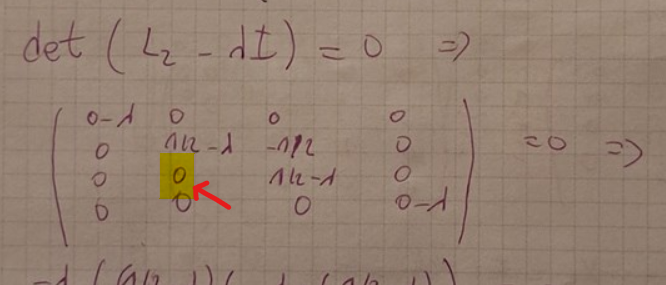Visa att L1 och L2 är diagonaliserbara med V1 och V2 och bestäm baser för dessa egenrum/egenvärden

Hej!
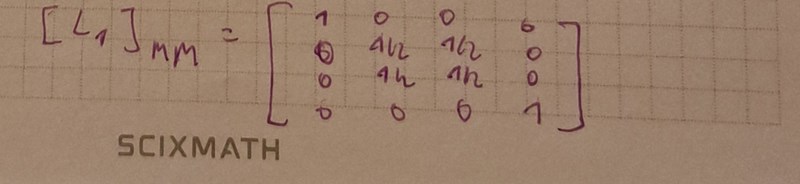
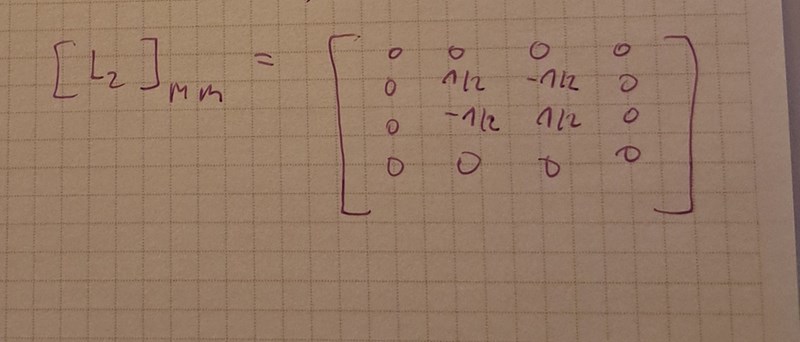
Jag fick dessa två matriser från d) uppgiften och undrar hur man ska visa att L1 och L2 är samtidigt diagonaliserbara? Vad menar man med egenrum V1 och V2?
Bestäm egenvärden och egenvektorer för och var för sig.
När det gäller , så inser du att alla egenvektorer till bildar ett linjärt underrum som sammanfaller med , så är egenrummet som hör ihop med . Sedan så består av alla egenvektorer till .
har alltså egenrummen till och till . (Det finns inga fler egenvärden)
När det gäller , så inser du att alla egenvektorer till bildar ett linjärt underrum som sammanfaller med , så är egenrummet som hör ihop med . Sedan så består av alla egenvektorer till .
har alltså egenrummen till och till . (Det finns inga fler egenvärden)
Operatorerna och har alltså likadana egenrum (till olika egenvärden, men det viktiga är att det handlar om likadana egenrum). Bestämmer du någon bas för dessa egenrum och byter bas hos både och , så har du diagonaliserat båda två med samma bas.
Alternativt bevis för samtidig diagonaliserbarhet: Notera att , där betecknar identitet. Har man en egenvektor (egenmatris) till med egenvärdet , så blir
d.v.s. denna är en egenvektor även till fast med egenvärdet . Därmed har och samma uppsättning av egenvektorer och även egenrum (fast med olika egenvärden). Bildar man bas av egenvektorer till , så är det en bas av egenvektorer även till .
 Såhär gjorde jag. Är mina egenvärden korrekta för L1?
Såhär gjorde jag. Är mina egenvärden korrekta för L1?

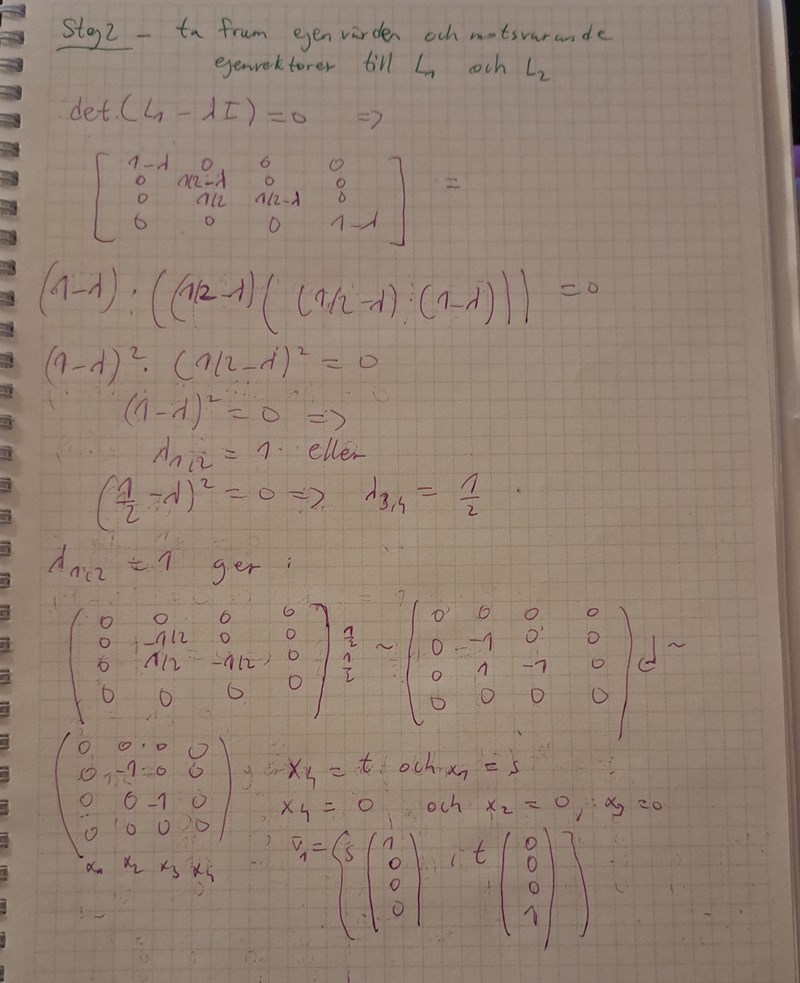
Du har tappat bort elementet 1/2 i matrisen för L1 på andra raden i tredje kolumnen respektive -1/2 i matrisen för L2 på tredje raden i andra kolumnen. Egenvärdena är därmed fel.

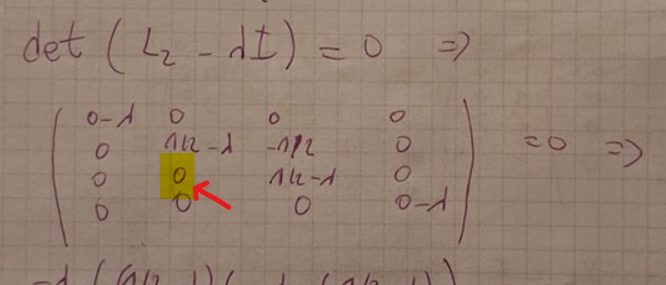
Som jag skrivit i mitt förra inlägg, så är egenvärdena 0 och 1 (och det finns inga fler egenvärden) hos både L1 och L2. De tillhörande egenrummen sammanfaller med underrummen V1 respektive V2
LuMa07 skrev:Du har tappat bort elementet 1/2 i matrisen för L1 på andra raden i tredje kolumnen respektive -1/2 i matrisen för L2 på tredje raden i andra kolumnen. Egenvärdena är därmed fel.
Som jag skrivit i mitt förra inlägg, så är egenvärdena 0 och 1 (och det finns inga fler egenvärden) hos både L1 och L2. De tillhörande egenrummen sammanfaller med underrummen V1 respektive V2
Nu har jag korrigerat detta. Såhär gjorde jag. Man ska tydligen multiplicera med (1-lambda) med matrisen men jag förstår inte varför man ska göra det och vad det har med determinanten att göra när man kofaktorutvecklar vid andra raden och andra kolumnen? Om man man multiplicerar med (1-lambda) så ska man lambda 1 dvs lambda1=lambda2 och lambda4=1 och lambda3=0. Men sen finns det ett litet problem när man ska hitta egenvektorer till lambda1=lamnda2=lambda4=1 , den blir ju 0 pga faktorn (1-lambda)

Underdeterminanten till elementet är den determinant som fås , då man stryker den rad och och den kolonn där står. Kofaktorn definieras av . Enligt utvecklingssatsen för determinanter kan du sedan utveckla längs en rad eller en kolonn. Då är determinanten en summa, till exempel utmed kolonn , . Det är särskilt bekvämt att utveckla längs en rad eller en kolonn som mest består av 0.
I det här fallet utvecklar vi först utmed rad 1 och sedan utmed den nya rad 3. Så här
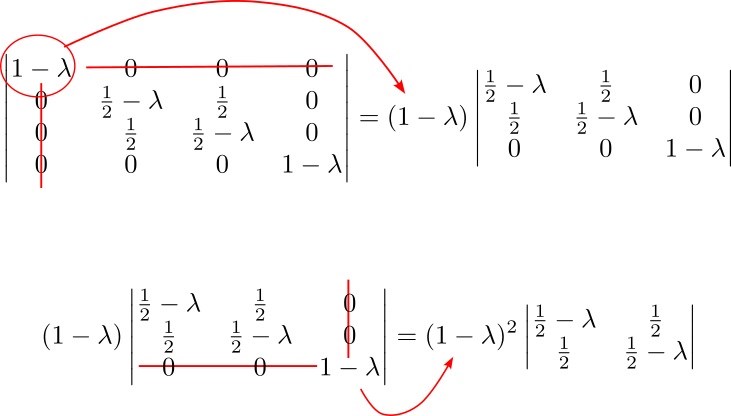
Slutligen får du ekvationen
Den har lösningarna samt .
Jag förstår inte hur du får egenvektorerna som hör till egenvärde till noll? Kanske kan du visa hur du räknar ut dem? De ska uppfylla ekvationen .
D4NIEL skrev:Underdeterminanten till elementet är den determinant som fås , då man stryker den rad och och den kolonn där står. Kofaktorn definieras av . Enligt utvecklingssatsen för determinanter kan du sedan utveckla längs en rad eller en kolonn. Då är determinanten en summa, till exempel utmed kolonn , . Det är särskilt bekvämt att utveckla längs en rad eller en kolonn som mest består av 0.
I det här fallet utvecklar vi först utmed rad 1 och sedan utmed den nya rad 3. Så här
Slutligen får du ekvationen
Den har lösningarna samt .
Jag förstår inte hur du får egenvektorerna som hör till egenvärde till noll? Kanske kan du visa hur du räknar ut dem? De ska uppfylla ekvationen .
Uppgiften löste sig. Jag slarvade lite på vägen.