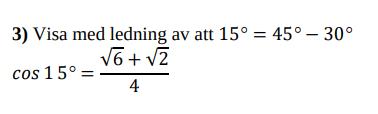Visa att ledning av att 15⁰ = 45⁰ - 30⁰.....

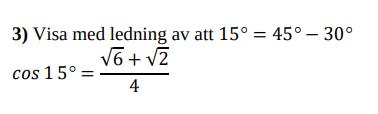
ii_noor06 skrev:

Hej,

Jag är jättefast med denna frågan. Har försökt så många gånger jag tycker att jag kan inte börja någonstans. Kan någon hjälpa mig för att kunna gå vidare med mina uppgifter.

Jag började i alla fall lista ut roten ur 6 + roten ur 2 sedan delat på 4.

$$\begin{gathered} \sqrt{6 }= 2.44948974278 \\ \sqrt{2}= 1.41421356237 \\ 2.44948974278 + 1.41421356237 = 3.86370330515 \\ \frac{ 3.86370330515}{4}= 0.965925826288 \\ 0.965925826288 \approx 0.97 \end{gathered}$$

Tack!

Nej, du är inte på rätt väg. Leta i din formelsamling efter en formel som visar vad cos(a+b) är, uttryckt i sin(a), sin(b), cos(a) och cos(b) (eller några av dem), och ta reda på värdena för sinus och cosinus för 30^o och 45^o, exakt.

Nej, du är inte på rätt väg. Leta i din formelsamling efter en formel som visar vad cos(a+b) är, uttryckt i sin(a), sin(b), cos(a) och cos(b) (eller några av dem),

Vart ska jag hitta den, letat mycket faktiskt 

och ta reda på värdena för sinus och cosinus för 30⁰ och 45^o, exakt.

$$\begin{gathered} \cos 30° =\frac{\sqrt{2}}{2} \\ \cos 45° =\frac{\sqrt{3}}{2} \\ \sin 30° =\frac{\sqrt{2}}{2} \\ \sin 45° =\frac{1}{2} \end{gathered}$$

ii_noor06 skrev:

Vart ska jag hitta den, letat mycket faktiskt 

Ladda gärna ner Skolverkets formelblad Matte 4, det är bra att bekanta sig med det inför proven.

Där står bland annat följande:

$$\begin{gathered} \cos 30° =\frac{\sqrt{2}}{2} \\ \cos 45° =\frac{\sqrt{3}}{2} \\ \sin 30° =\frac{\sqrt{2}}{2} \\ \sin 45° =\frac{1}{2} \end{gathered}$$

Nej, det stämmer inte.

Lite längre ner i ovan nämnda formelblad står följande:

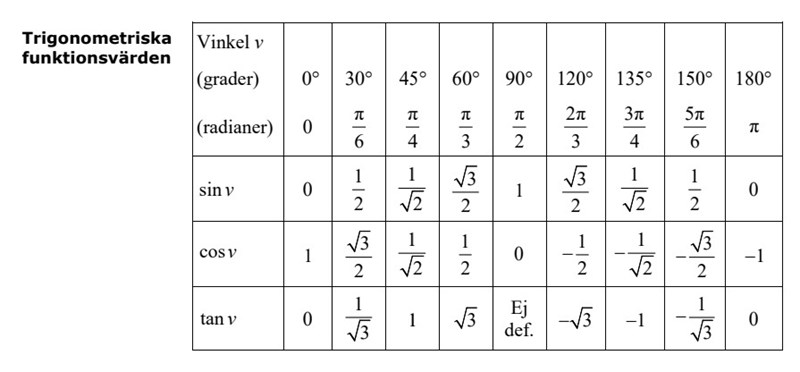
Jag hittade den här och skrev utav den jag hittade. Dock märkte jag nyss att jag skrev fel. Blandade ihop de.

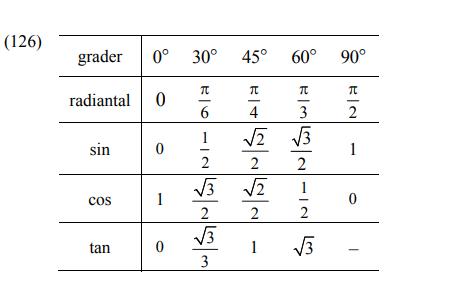
Cos 45⁰ =1 /roten ur 2

Cos 30⁰ = roten ur 3 / 2

Sin 45⁰ = 1 / roten ur 2

Sin 30⁰ = 1 / 2

Hittade du en lämplig formel i Yngves inlägg #4?

Ja, femte raden

cos(u-v)= cos u cos v + sin u sin v 

ii_noor06 skrev:

Ja, femte raden

cos(u-v)= cos u cos v + sin u sin v 

Bra. Visa dina uträkningar.

$$\begin{gathered} \cos (15°) = \cos (45°-30°) = \cos (45°) \cos (30°)+\sin (45°) \sin )30°) \\ ?? \end{gathered}$$

Tillägg: 20 jan 2024 19:51

(30⁰)**

OK det stämmer.

Och vad får du för resultat?

Som jag listade ut innan så vet jag de olika 

Cos 45⁰ =1 /roten ur 2

Cos 30⁰ = roten ur 3 / 2

Sin 45⁰ = 1 / roten ur 2

Sin 30⁰ = 1 / 2

Så tror jag att det blir så här.

$$\begin{gathered} \frac{1}{\sqrt{2}}* \frac{\sqrt{3}}{2}+ \frac{1}{2}*\frac{1}{2} = ( \frac{1}{\sqrt{2}}*\frac{\sqrt{3}}{2}) + (\frac{1}{\sqrt{2}}*\frac{1}{2}) * \frac{\sqrt{2}}{\sqrt{2}}= \\ = \frac{1}{\sqrt{2}}*\frac{\sqrt{3}}{2}*\frac{\sqrt{2}}{\sqrt{2}}+\frac{1}{\sqrt{2}}*\frac{1}{2}* \frac{\sqrt{2}}{\sqrt{2}}= \\ = \frac{\sqrt{3} *\sqrt{2}}{4} + \frac{\sqrt{2}}{4} = \frac{\sqrt{6}}{4}+ \frac{\sqrt{2}}{4}= \\ \frac{\sqrt{6 }+\sqrt{2}}{4} \end{gathered}$$

Ja, det stämmer. Bra!

Yngve skrev:

Ja, det stämmer. Bra!

okej tack!