Visa att mängden V är ett vektorrum

Ta två vektorer, u och v, och två skalärer, a och b.

Visa att vektorn w = au + bv ligger i vektorrummet om u och v ligger i vektorrummet.

Dr. G skrev:

Ta två vektorer, u och v, och två skalärer, a och b.

Visa att vektorn w = au + bv ligger i vektorrummet om u och v ligger i vektorrummet.

Kan jag välja tex v=x^2, u=x, b=1, a=2. Isåfall w=2x+1*x^2=2x+x^2 och eftersom gradtalet är 2 ligger w i vektorrummet

Eller ska man inte sätta in några värden på dem?

Du ska ta två godtyckliga vektorer u och v som ligger i vektorrummet, d.v.s u är ett (godtyckligt) polynom av grad max n och v är ett annat. 

Påverkar multiplikation med skalär polynomets grad?

Kan graden bli > n när du summerar två polynom av grad ≤ n?

Dr. G skrev:

Du ska ta två godtyckliga vektorer u och v som ligger i vektorrummet, d.v.s u är ett (godtyckligt) polynom av grad max n och v är ett annat. 

Påverkar multiplikation med skalär polynomets grad?

Kan graden bli > n när du summerar två polynom av grad ≤ n?

Okej,

nej, men hur visar jag det? Vet inte om det är tänkt så som jag gjort på bilden?

• Du ska ta två polynom $p$ och $q$, av grad som mest $n$, och visa att $p+q$ är ett polynom av grad som mest $n$.
• Du ska ta ett polynom $p$, av grad som mest $n$, och ett tal $\alpha$ och visa att $\alpha \cdot p$ är ett polynom av grad som mest $n$.

Visa att om $grad(p)\leq n$ och $grad(q)\leq n$ så är $p+q$ ett polynom och $grad(p+q)\leq n$.

Visa att om $grad(p)\leq n$ så är $\alpha \cdot p$ ett polynom och $grad(\alpha \cdot p)\leq n$.

Albiki skrev:

Visa att om $grad(p)\leq n$ och $grad(q)\leq n$ så är $p+q$ ett polynom och $grad(p+q)\leq n$.

Visa att om $grad(p)\leq n$ så är $\alpha \cdot p$ ett polynom och $grad(\alpha \cdot p)\leq n$.

Ser det här okej ut?

Nej, (x⁰+x¹)(a₀+a₁+b₀+b₁) är ju inte a₀x⁰ + a₁x¹ + b₀x⁰ + b₁x¹.

Laguna skrev:

Nej, (x⁰+x¹)(a₀+a₁+b₀+b₁) är ju inte a₀x⁰ + a₁x¹ + b₀x⁰ + b₁x¹.

Juste,

blir det såhär?

Det var bättre. 

Laguna skrev:

Det var bättre. 

Ska jag visa att de 8 axiomen uppfylls också?

Tex att u+v=v+u

Känns inte som det är så mycket att visa med axiomen, eller har jag fel?

Här är ju axiomen

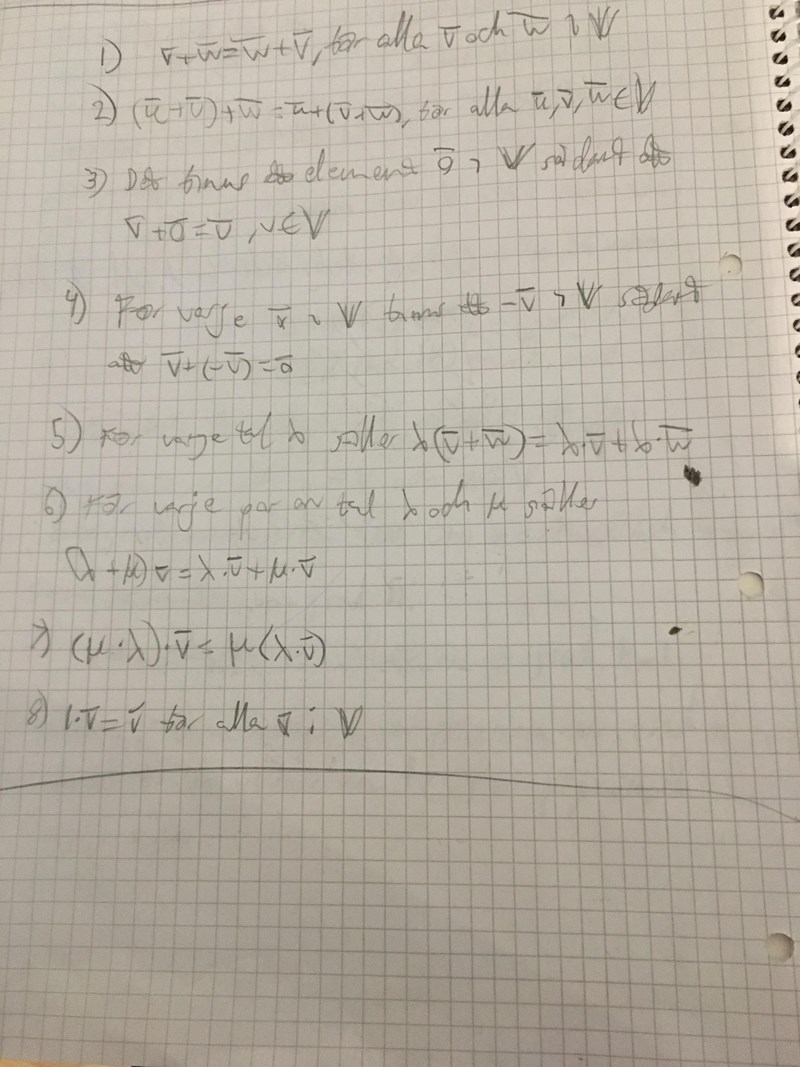
Såhär gjorde jag

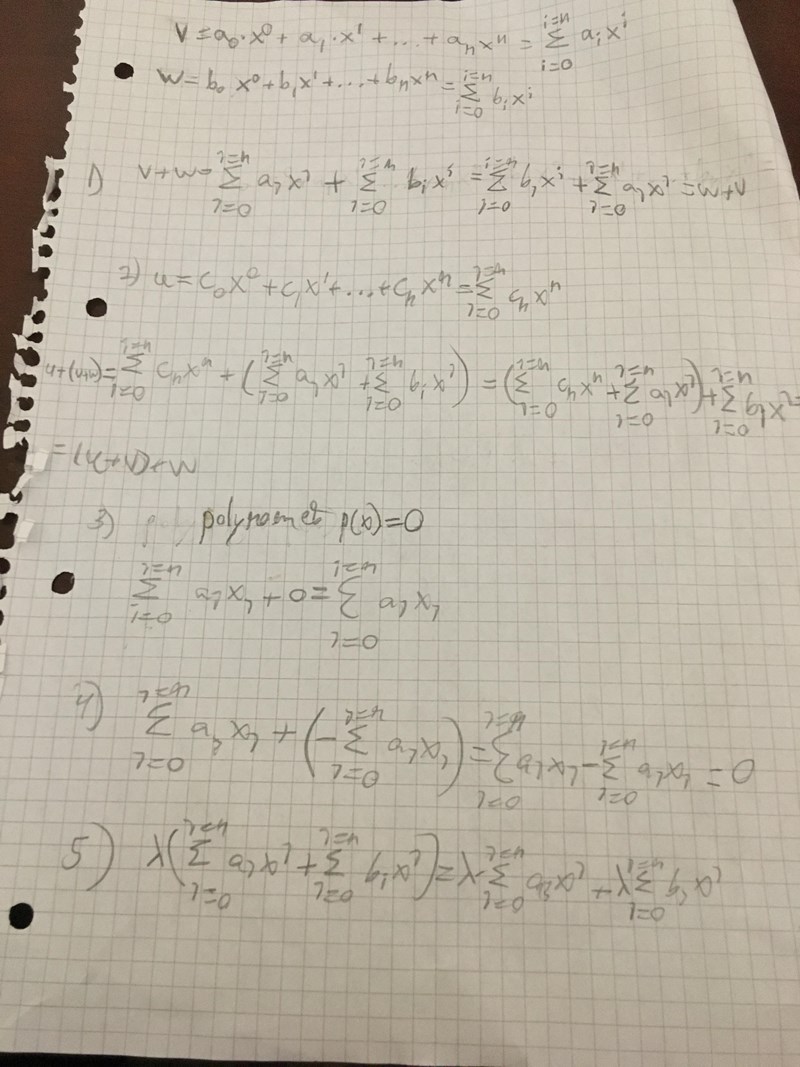
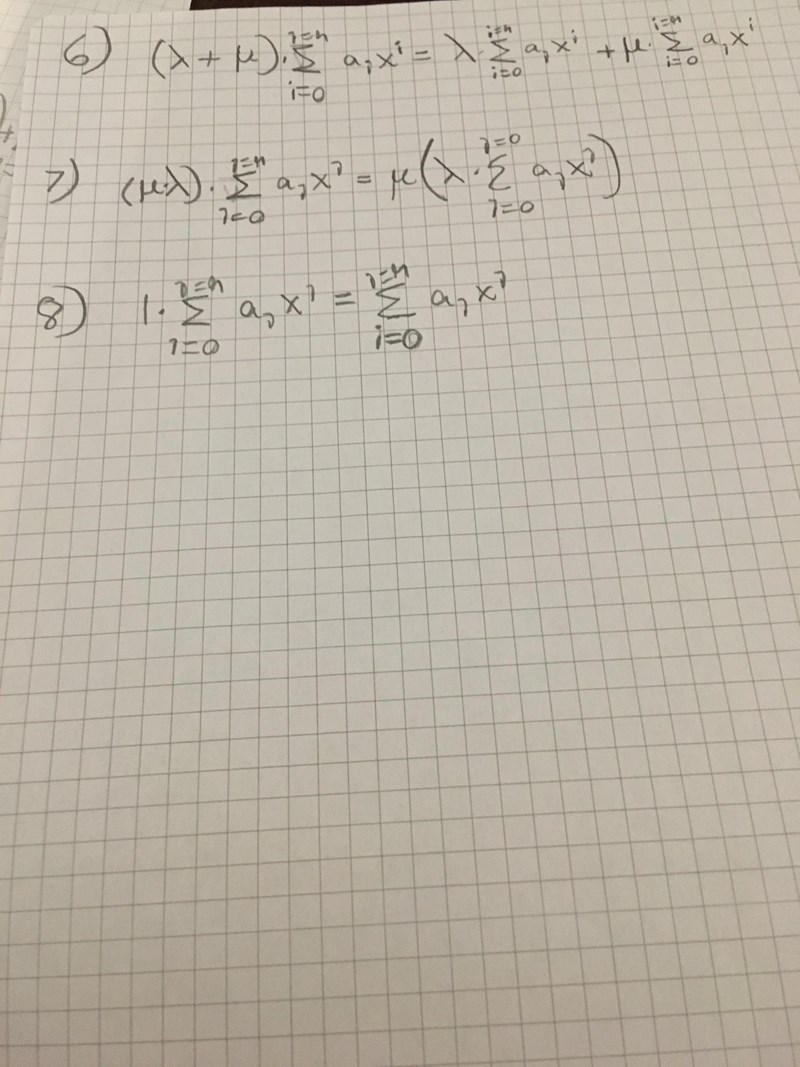
Spelar det egentligen någon roll att graden ska vara som mest $n$? Om $W$ är mängden av alla polynom av grad exakt lika med $n$, är $W$ ett vektorrum? Om svaret är Nej, varför inte?

Albiki skrev:

Spelar det egentligen någon roll att graden ska vara som mest $n$? Om $W$ är mängden av alla polynom av grad exakt lika med $n$, är $W$ ett vektorrum? Om svaret är Nej, varför inte?

Nej det är inte ett vektorrum om det är exakt lika med n eftersom vektorrummet inte är slutet under addition då. Om man adderar tex x+x^2 och -x^2 blir gradtalet 1 och inte 2.

lamayo skrev:

Albiki skrev:

Spelar det egentligen någon roll att graden ska vara som mest $n$? Om $W$ är mängden av alla polynom av grad exakt lika med $n$, är $W$ ett vektorrum? Om svaret är Nej, varför inte?

Nej det är inte ett vektorrum om det är exakt lika med n eftersom vektorrummet inte är slutet under addition då. Om man adderar tex x+x^2 och -x^2 blir gradtalet 1 och inte 2.

Det är sant. Mängden är inte sluten under skalärmultiplikation heller eftersom om man multiplicerar $x+x^2$ med skalären $0$ fås nollpolynomet, som inte är ett polynom av grad exakt lika med $2$.

Vad betyder det egentligen att vara ett polynom?

Är exempelvis $(\sin x)^2+2\sin x$ ett polynom?

Albiki skrev:

Visa att om $grad(p)\leq n$ och $grad(q)\leq n$ så är $p+q$ ett polynom och $grad(p+q)\leq n$.

Visa att om $grad(p)\leq n$ så är $\alpha \cdot p$ ett polynom och $grad(\alpha \cdot p)\leq n$.

Notera följande räkneregler för polynomgrader:

    $grad(p+q) =max(grad(p),grad(q))$

och

    $grad(\alpha \cdot p) = grad(p)$ om talet $\alpha \neq 0$.

Albiki skrev:

Vad betyder det egentligen att vara ett polynom?

Är exempelvis $(\sin x)^2+2\sin x$ ett polynom?

Ja, det är ett polynom. 

Det består av konstanter, variabler, heltalsexpontenter (positiva) och kan kombineras med de fyra räknesätten förutom division.

lamayo skrev:

Albiki skrev:

Vad betyder det egentligen att vara ett polynom?

Är exempelvis $(\sin x)^2+2\sin x$ ett polynom?

Ja, det är ett polynom. 

Det består av konstanter, variabler, heltalsexpontenter (positiva) och kan kombineras med de fyra räknesätten förutom division.

Nej, det är inte ett polynom. Att säga att något "är ett polynom" räcker inte som specifikation.

• Uttrycket $(\sin x)^2+2\sin x$ är inte ett polynom med avseende på $x$.
• Uttrycket $(\sin x)^2+2\sin x$ är ett polynom med avseende på $\sin x$.

Albiki skrev:

lamayo skrev:

Visa föregående citat

Albiki skrev:

Vad betyder det egentligen att vara ett polynom?

Är exempelvis $(\sin x)^2+2\sin x$ ett polynom?

Ja, det är ett polynom. 

Det består av konstanter, variabler, heltalsexpontenter (positiva) och kan kombineras med de fyra räknesätten förutom division.

Nej, det är inte ett polynom. Att säga att något "är ett polynom" räcker inte som specifikation.

• Uttrycket $(\sin x)^2+2\sin x$ är inte ett polynom med avseende på $x$.
• Uttrycket $(\sin x)^2+2\sin x$ är ett polynom med avseende på $\sin x$.

Aha!

Albiki skrev:

Albiki skrev:

Visa att om $grad(p)\leq n$ och $grad(q)\leq n$ så är $p+q$ ett polynom och $grad(p+q)\leq n$.

Visa att om $grad(p)\leq n$ så är $\alpha \cdot p$ ett polynom och $grad(\alpha \cdot p)\leq n$.

Notera följande räkneregler för polynomgrader:

    $grad(p+q) =max(grad(p),grad(q))$

och

    $grad(\alpha \cdot p) = grad(p)$ om talet $\alpha \neq 0$.

Ska jag använda de för att visa att de 8 axiomen uppfylls?

lamayo skrev:

Albiki skrev:

Visa föregående citat

Albiki skrev:

Visa att om $grad(p)\leq n$ och $grad(q)\leq n$ så är $p+q$ ett polynom och $grad(p+q)\leq n$.

Visa att om $grad(p)\leq n$ så är $\alpha \cdot p$ ett polynom och $grad(\alpha \cdot p)\leq n$.

Notera följande räkneregler för polynomgrader:

    $grad(p+q) =max(grad(p),grad(q))$

och

    $grad(\alpha \cdot p) = grad(p)$ om talet $\alpha \neq 0$.

Ska jag använda de för att visa att de 8 axiomen uppfylls?

Det kan du, men det primära syftet är att använda dem för att visa att V är sluten under polynomaddition och under skalärmultiplikation.

Notera att varje element i $V$ kan representeras med en vektor av reella tal:

    $p(x) = a_0+a_1x+\cdots+a_nx^n \iff (a_0,a_1,\ldots,a_{n})\in\mathbb{R}^{n+1}.$

Vektorrummet $V$ har samma algebraiska struktur som vektorrummet $\mathbb{R}^{n+1}$. Ovanstående specifikation är ett exempel på isomorfism mellan de två vektorrummen. 

Albiki skrev:

lamayo skrev:

Visa föregående citat

Albiki skrev:

Albiki skrev:

Visa att om $grad(p)\leq n$ och $grad(q)\leq n$ så är $p+q$ ett polynom och $grad(p+q)\leq n$.

Visa att om $grad(p)\leq n$ så är $\alpha \cdot p$ ett polynom och $grad(\alpha \cdot p)\leq n$.

Notera följande räkneregler för polynomgrader:

    $grad(p+q) =max(grad(p),grad(q))$

och

    $grad(\alpha \cdot p) = grad(p)$ om talet $\alpha \neq 0$.

Ska jag använda de för att visa att de 8 axiomen uppfylls?

Det kan du, men det primära syftet är att använda dem för att visa att V är sluten under polynomaddition och under skalärmultiplikation.

Om vi väljer två godtyckliga polynom p och q i V av grad max n så kommer enligt den första räkneregeln grad(q+p) = eller mindre än n och enligt den andra räkneregeln grad(lamda*p)= eller mindre än n, lambda olikt 0. Alltså är V sluten under skalärmultiplikation och addition.

Albiki skrev:

Notera att varje element i $V$ kan representeras med en vektor av reella tal:

    $p(x) = a_0+a_1x+\cdots+a_nx^n \iff (a_0,a_1,\ldots,a_{n})\in\mathbb{R}^{n+1}.$

Vektorrummet $V$ har samma algebraiska struktur som vektorrummet $\mathbb{R}^{n+1}$. Ovanstående specifikation är ett exempel på isomorfism mellan de två vektorrummen. 

Vad innebär algebraisk struktur? Vad kan jag använda det till?