1
svar
118
visningar
Visa att med absolutbelopp
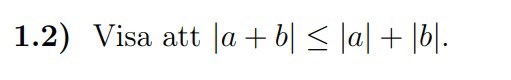
Jag antar att man ska göra olika alternativ för att a och b kan vara både negativa och positiva men jag förstår inte alls hur man ska göra.
Visa spoiler

Här är ett alternativ om man tycker det är jobbigt med alla alternativ.
Lemma 1. |x|2 = x2 för alla reella x. Bevis: Trivialt.
Lemma 2. x |x| för alla reella x. Bevis: Trivialt.
Lemma 3. |xy| = |x||y| för alla reella och y. Bevis: använd tex lemma 1.
|a + b|2 = (a + b)2 = a2 + b2 + 2ab = |a|2 + |b|2 + 2ab |a|2 + |b|2 + 2|ab| = |a|2 + |b|2 + 2|a||b| = (|a| + |b|)2.
Således har vi att |a + b|2 (|a| + |b|)2. Vilket ger det sökta resultatet om vi drar roten ur på båda sidor. Roten ur är en strikt växande funktion, så olikheten bevaras när vi drar roten ur.


