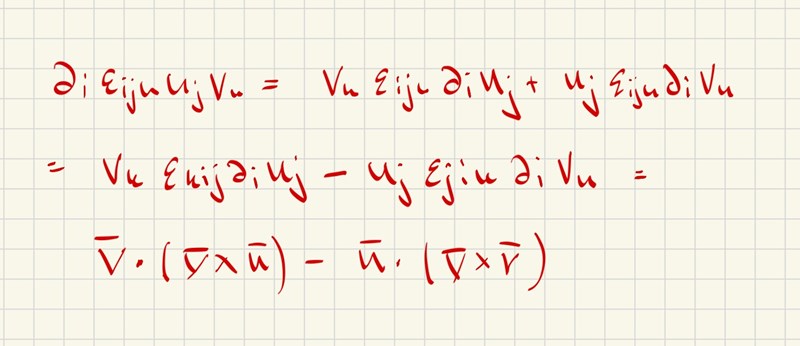Visa att nabla*(u×v) med c1 och c2 okända

Hej!

Jag skulle vilja använda mig av indexräkning för att jobba med VL men är fast vid hur man ska bestämma c1 och c2.

såhär långt kom jag först. d_ie_jklu_kv_l=e_jkld_i(u_kv_l)=e_jkl(v_ld_iu_k+u_kd_iv_l)

$\nabla ∙ (\vec{u} \times \vec{v}) = \partial_{j} ε_{j k l} u_{k} v_{l}$

PATENTERAMERA skrev:
$\nabla ∙ (\vec{u} \times \vec{v}) = \partial_{j} ε_{j k l} u_{k} v_{l}$

Varför har differentialoperatorn en j och inte i som jag hade ? spelar det någon roll om första bokstaven i epsilon har j eller tex k?

Ja det spelar roll. Divergensen av en vektor är en skalär (noll fria index). Du har två fria index (andra ordningens tensor). Hänger du med?

PATENTERAMERA skrev:
Ja det spelar roll. Divergensen av en vektor är en skalär (noll fria index). Du har två fria index (andra ordningens tensor). Hänger du med?

Ja juste. Skalärer har ingen fria index medan vektorer har det , men vilka är då de två fria index som uppkommer pga kryssprodukten mellan u och v? (Tror jag har glömt detta lite ). Vad innebär andra ordningens tensor?

Du har fått till två fria index: i och j. En andra ordningens tensor har två fria index. En första ordningens tensor (en vektor) har ett fritt index. En skalär har noll fria index.

div(uxv) = d_j(uxv)_j = d_je_jklu_kv_l=… .

PATENTERAMERA skrev:
Du har fått till två fria index: i och j. En andra ordningens tensor har två fria index. En första ordningens tensor (en vektor) har ett fritt index. En skalär har noll fria index.

div(uxv) = d_j(uxv)_j = d_je_jklu_kv_l=… .

Ja ok jag förstår. Så långt har jag kommit. Blir inte allt 0 här?

$\partial_{i} u_{j} \neq δ_{i j}$ .

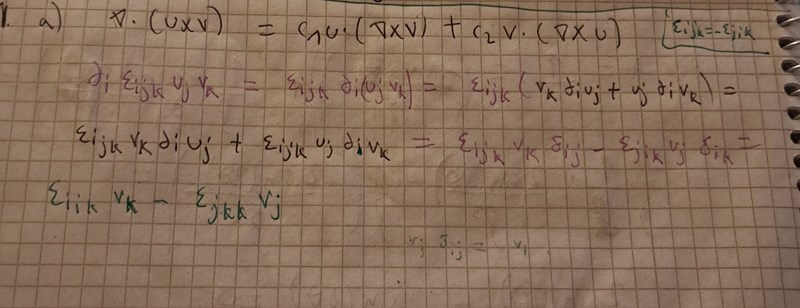
PATENTERAMERA skrev:
$\partial_{i} u_{j} \neq δ_{i j}$ .

Varför inte? Eller är det typ om man har ujd_i som är det eller är det mest om vi råkar ha d_jr_i?

Hur bestämmer jag konstanterna c1 och 2? Från sista raden verkar det vara så att c1=c2 är 1 men jag kan ha fel.

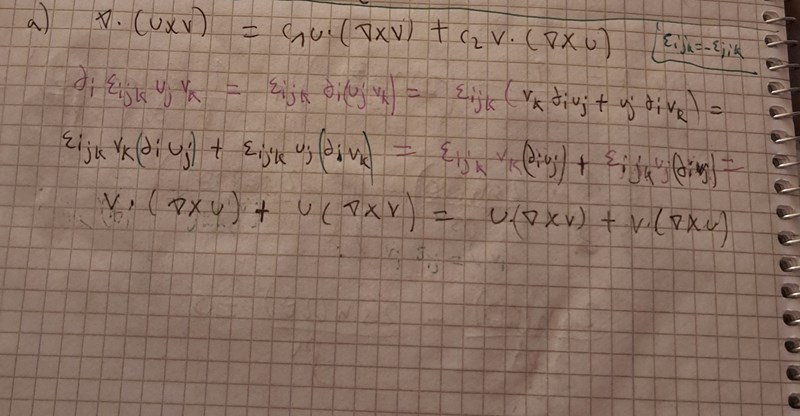
PATENTERAMERA skrev:

Vad händer i andra raden? Jag är inte riktigt med.

Utnyttja att e_ijk = e_kij och att e_ijk = -e_jik.

PATENTERAMERA skrev:
Utnyttja att e_ijk = e_kij och att e_ijk = -e_jik.

Fast jag förstår inte när minustecknet dyker upp och när det inte gör det?

Hur menar du? Det är väl klart var det blir minus. I första termen på rad 1 så byter vi e_ijk mot e_kij och i andra termen byter vi e_ijk mot -e_jik. Då får vi det som står på andra raden.

PATENTERAMERA skrev:
Hur menar du? Det är väl klart var det blir minus. I första termen på rad 1 så byter vi e_ijk mot e_kij och i andra termen byter vi e_ijk mot -e_jik. Då får vi det som står på andra raden.

Jag tror inte jag förstår riktigt varför det saknas minustecken vid det här bytet. Om vi har eijk=-ejik eller om vi har eijk=-ekji. Sen har jag svårt att hänga med på ditt byte varför det ser ut som det gör och varför du gör på det sättet. Jag tänkte att man följer det här nedan. Så egentligen borde du ha minus framför ekij eftersom eijk=-ekij enligt nedan och eijk=-ejik om man ska behandla udda och jämn permutationer.

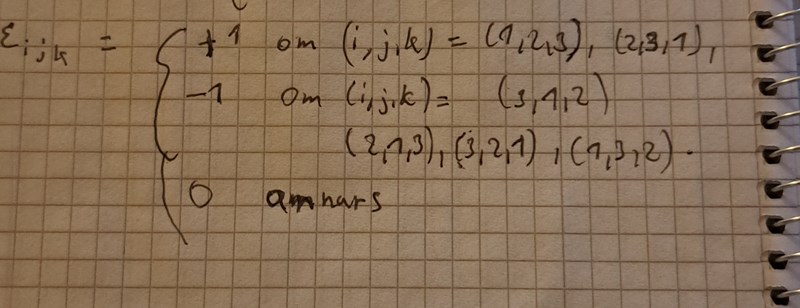
kij är en jämn permutation av ijk eftersom du kan få den genom att byta plats på index två gånger. Byt först plats på k och i och byt sedan plats på i och j.

jik är en udda permutation av ijk eftersom den kan fås genom att byta plats på i och j.

PATENTERAMERA skrev:
kij är en jämn permutation av ijk eftersom du kan få den genom att byta plats på index två gånger. Byt först plats på k och i och byt sedan plats på i och j.

jik är en udda permutation av ijk eftersom den kan fås genom att byta plats på i och j.

Du menar eijk=ekji=ekij vilket är jämn permutation av (123)=(321)=(312)? I din lösning gjorde du det bytet endast en gång men måste man göra det två gånger för att nå dit eller kan man bara göra det en gång?

En jämn permutation så måste du byta plats på index (transponera) ett jämnt antal gånger. För udda permutationer blir det ett udda antal.

e_ijk = e_kij = e_jki. e_ijk = -e_jik = -e_kji = -e_ikj.

PATENTERAMERA skrev:
En jämn permutation så måste du byta plats på index (transponera) ett jämnt antal gånger. För udda permutationer blir det ett udda antal.

e_ijk = e_kij = e_jki. e_ijk = -e_jik = -e_kji = -e_ikj.

Det är väldigt lätt att göra fel härifrån för min del. Jag minns som starkast att eijk=-ejik. När det gäller jämn antal gång man man byter plats antar jag att det är 1 , 2 ,4 och sen för udda antal gånger är det 2,3,7.

Svara

Visa senaste svar