Visa att olikheten alltid gäller

Hej,

Fråga 2315 a)

Har jag gjort rätt eller är jag ute och cyklar?

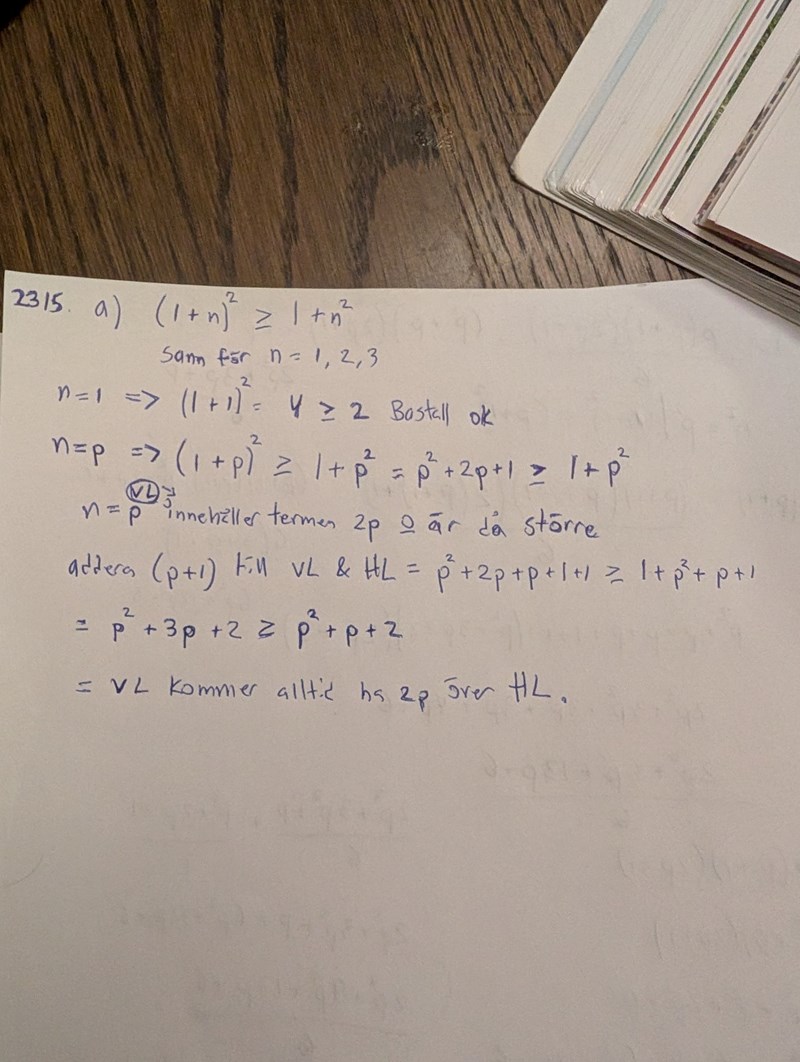
.kom på att man måste väl ha med n = p+1 på något sätt också. Och det man ska addera som jag gjorde ovan är väl i så fall att addera det jag la till nedan på både VL och HL?

Eller måste man ena addera någonting? :/ jag vet inte..

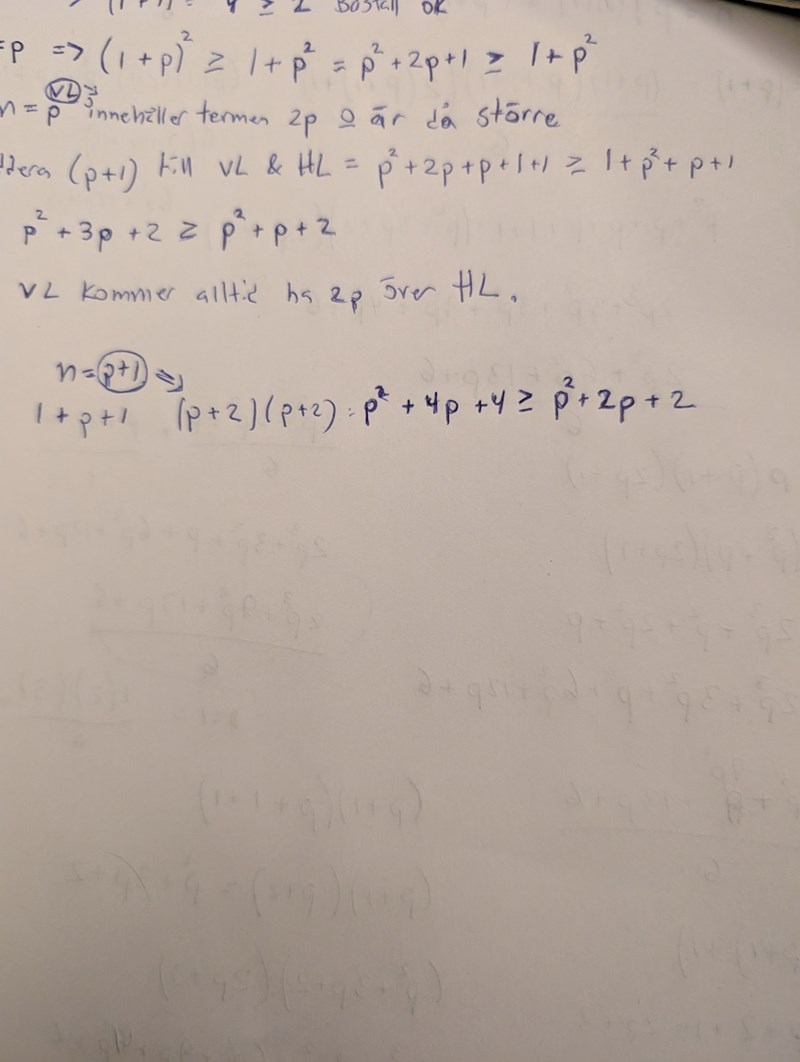
Jag tycket det är en konstig olikhet på induktionsdelen eftersom det är 100 gånger snabbare att visa detta utan induktion.

$(1+n)^2 = 1 + 2n + n^2 \geq 1+n^2$

Klart!

I induktionsbevis är andra steget att man antar att det gäller för n=p. Sedan ska man visa att det gäller för n=p+1 om antagandet gäller. Du ska anta att $(1+p)^2 \geq 1 + p^2$ Visa att $(1+(p+1))^2 \geq 1 + (p+1)^2$

Har jag inte gjort så?

Jag tror jag har gjort det rätt, ändå.

Man behöver ju också bara ett enda exempel egentligen..

Jag fattar i vilket fall, så jag är nöjd. Tack.

Svara

Visa senaste svar