Visa att tan x > sin x för alla x i 0 < x < pi/2 grader
Hej, jag ska visa att tan x > sin x för alla x i 0 < x < pi/2 och jag började med att rita en rätvinklig triangel. Men jag visst inte hur jag skulle fortsätta sedan.
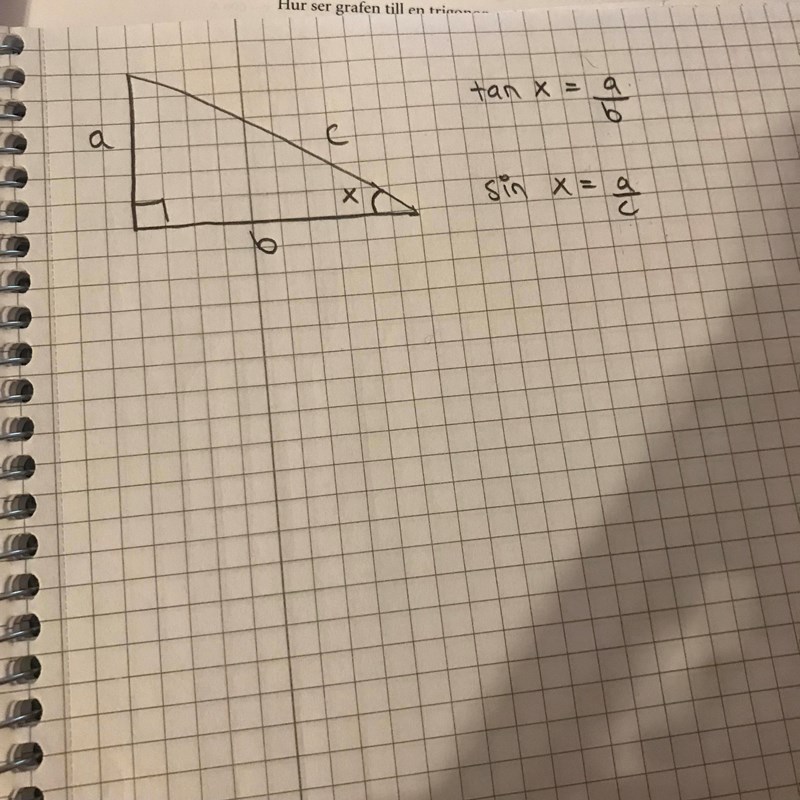
Då vill du alltså visa att
a/b > a/c
i vilken rätvinklig triangel som helst. Hur vet man att det gäller?
För att det ska gälla måste väll b vara mindre än c?
Ja, precis.
Är det bara så man resonerar, att b måste vara mindre än c för att tan x > sin x med tanke på att det är en A-fråga? :)
Logiskt sett bör man göra detta i omvänd ordning. Du ska visa att tan(x) > sin(x), där x är en spetsig vinkel i en rätvinklig triangel.
Rita figuren. Du vet att hypotenusan är längre än kateterna (annars får du använda en gammal greks sats).
c > b
invertera och byt håll på olikheten
1/c < 1/b
Multiplicera med det positiva talet a
a/c < a/b
vilket är samma sak som
sin(x) < tan(x)
En annan variant är att först visa att 0 < cos(x) < 1.
Okej, tack för hjälpen :)



