Visa att uttryck är heltal om n är ett heltal
Hej!
Har problem med fråga (64). Har utvecklat den till n²(n²+2n+1)/4
Det jag vet är att täljaren alltid blir heltal, men hur vet jag att hela uttrycket alltid blir ett heltal?

Anonym2005 skrev:Hej!
Har problem med fråga (64). Har utvecklat den till n²(n²+2n+1)/4
Det jag vet är att täljaren alltid blir heltal, men hur vet jag att hela uttrycket alltid blir ett heltal?
Det betyder att du skall visa att täljaren kan skrivas som 4.nånting.
Smaragdalena skrev:Anonym2005 skrev:Hej!
Har problem med fråga (64). Har utvecklat den till n²(n²+2n+1)/4
Det jag vet är att täljaren alltid blir heltal, men hur vet jag att hela uttrycket alltid blir ett heltal?
Det betyder att du skall visa att täljaren kan skrivas som 4.nånting.
Låter rimligt! Men jag har faktoriserat så långt det bara går?
Smaragdalena skrev:Anonym2005 skrev:Hej!
Har problem med fråga (64). Har utvecklat den till n²(n²+2n+1)/4
Det jag vet är att täljaren alltid blir heltal, men hur vet jag att hela uttrycket alltid blir ett heltal?
Det betyder att du skall visa att täljaren kan skrivas som 4.nånting.
Räcker det med att bevisa att det är delbart med 1,2,3 och 4? Men då saknar jag ju primtal såsom 7 och 11...
Nej det går inte ens.
Det du behöver göra är att visa att täljaren alltid innehåller faktorerna 2*2 (och lite fler)
Du behöver bara visa att täljaren är delbar med 4, Då kommer den automatiskt vara delbar med 2 och 1. Det finns ingen snledning att tro att den skall vara delbar med 3, 5, 7 eller något annat tal.
Smaragdalena skrev:Du behöver bara visa att täljaren är delbar med 4, Då kommer den automatiskt vara delbar med 2 och 1. Det finns ingen snledning att tro att den skall vara delbar med 3, 5, 7 eller något annat tal.
Ska jag använda induktion?
Ska jag använda induktion?
Nej, du skall bara visa att täljaren är delbar med 4.
Tänk på att om n är udda så är n+1 jämnt, och tvärtom.
Smaragdalena skrev:Ska jag använda induktion?
Nej, du skall bara visa att täljaren är delbar med 4.
Tänk på att om n är udda så är n+1 jämnt, och tvärtom.
Jag slarvade, ska fixa misstaget först!
Smaragdalena skrev:Ska jag använda induktion?
Nej, du skall bara visa att täljaren är delbar med 4.
Tänk på att om n är udda så är n+1 jämnt, och tvärtom.
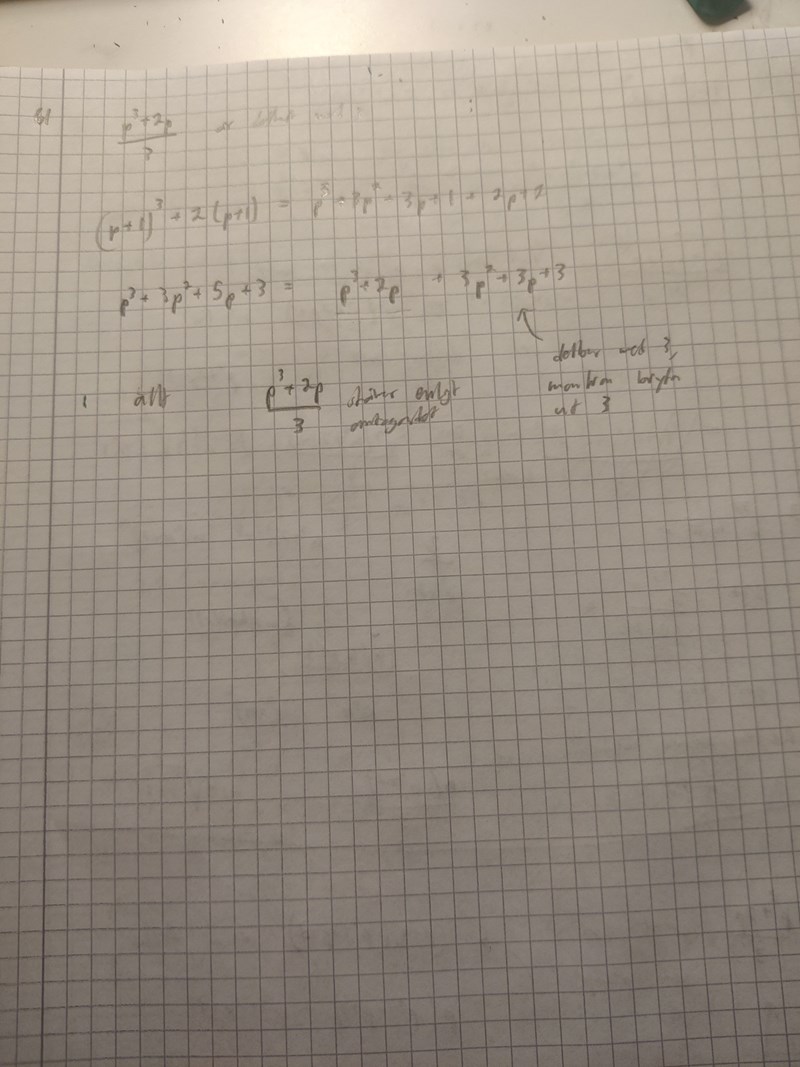
Anonym2005 skrev:Smaragdalena skrev:Ska jag använda induktion?
Nej, du skall bara visa att täljaren är delbar med 4.
Tänk på att om n är udda så är n+1 jämnt, och tvärtom.
INTE IGEENNNN. Slarvfel igen! Ska fixa det!
Oj, de menade 4...
Anonym2005 skrev:Smaragdalena skrev:Ska jag använda induktion?
Nej, du skall bara visa att täljaren är delbar med 4.
Tänk på att om n är udda så är n+1 jämnt, och tvärtom.
Jaha oj! hehe. Jag höll på med att lösa en annan uppgift, medan jag frågade. Det står "61" där uppe. Ska göra 64 denna gång.
Smaragdalena skrev:Anonym2005 skrev:Hej!
Har problem med fråga (64). Har utvecklat den till n²(n²+2n+1)/4
Det jag vet är att täljaren alltid blir heltal, men hur vet jag att hela uttrycket alltid blir ett heltal?
Det betyder att du skall visa att täljaren kan skrivas som 4.nånting.
Jag gör en ny tråd, jag har slarvat mellan uppgifter och i uppgifterna. Har iaf en uträkning/bevis med hjälp av induktion
Nej, om du gör en ny tråd om samma fråga kommer bara moderatorerna låsa den.
Smaragdalena skrev:Nej, om du gör en ny tråd om samma fråga kommer bara moderatorerna låsa den.
Okej!






