Visa följande formler som kallas eulers formler.

Enligt facit så ska cosx och cos(-X) adderas och sinx ska subtraheras med sin(-x), så att man får det till 2cosx *0,5. Är det någon här som vet varför det blir så kan du isf snälla förklara? Det här är en röd uppgift d.v.s. svår.

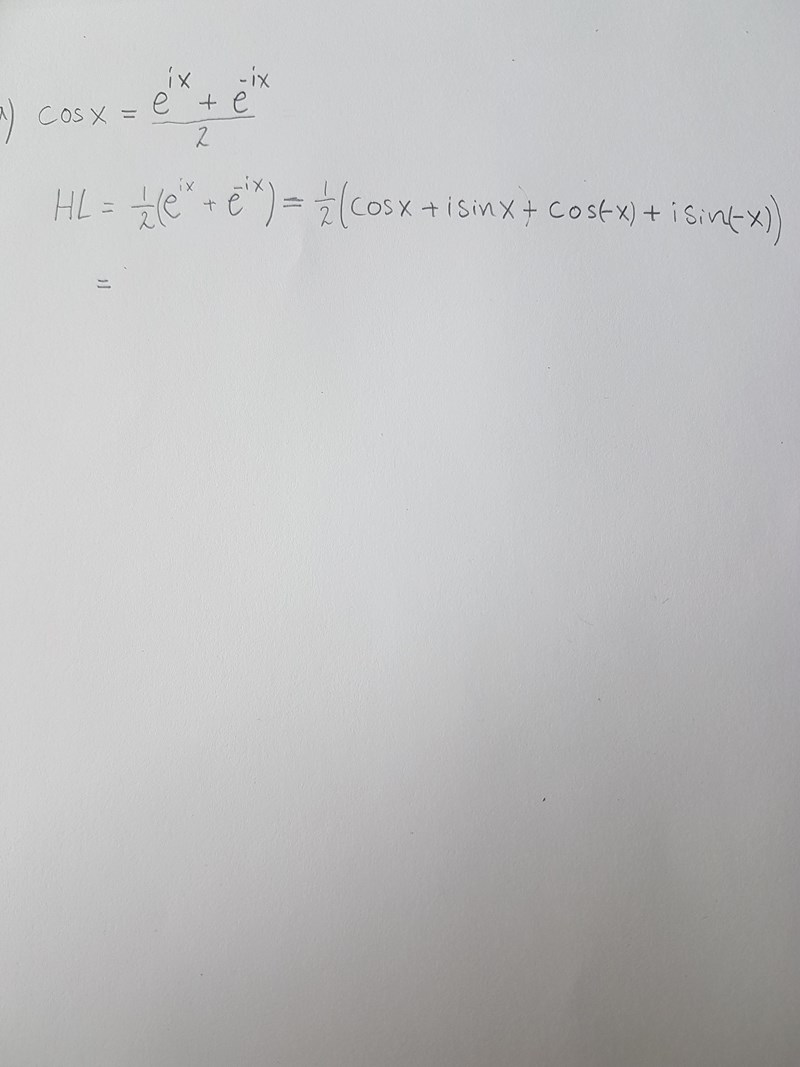
Hej!

Det gäller att $\cos{\left(-x\right)}=\cos{\left(x\right)}$ och $\sin{\left(-x\right)}=-\sin{\left(x\right)}$ . Använd det och se vad du får.

Moffen skrev:
Hej!

Det gäller att $\cos{\left(-x\right)}=\cos{\left(x\right)}$ och $\sin{\left(-x\right)}=-\sin{\left(x\right)}$ . Använd det och se vad du får.

Okej, tack. Men vad är det som gör att dessa villkor gäller?

Inspiredbygreatness skrev:
Moffen skrev:
Hej!

Det gäller att $\cos{\left(-x\right)}=\cos{\left(x\right)}$ och $\sin{\left(-x\right)}=-\sin{\left(x\right)}$ . Använd det och se vad du får.

Okej, tack. Men vad är det som gör att dessa villkor gäller?

Nevermind, förklaringen är relationerna mellan koordinationerna och kvadranterna.

Tack ändå

Svara

Visa senaste svar