Visa likeheten

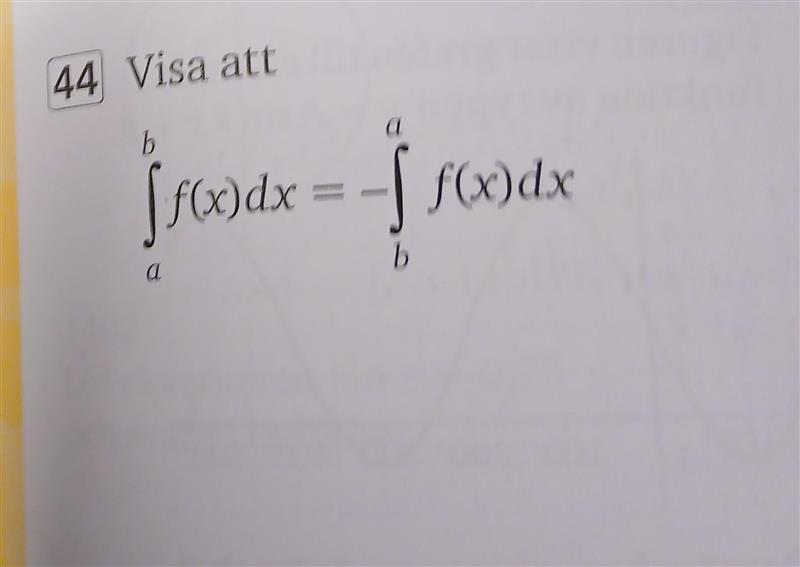
Jag vet inte hur man kan visa det här utan att göra visuellt. Eftersom det handlar väl om att förstå hur integralen blir negativ om vi befinner oss under x-axeln ?

Jag skulle säga att detta är en definition man ska känna till som fakta.

Enda sättet man kan 'bevisa' det är att gå via integralkalkylens fundamentalsats (men i beviset av det har man redan utgått från att detta är en implicit definition.

Hursomhelst

$\int_a^b f dx = F(b) - F(a)$

Om $F$ är en primitiv till $f$ så kommer $-F$ att vara en primitiv till $-f$.

Därmed har vi att

$-\int_b^a f(x) dx = \int_b^a -f(x) dx = (-F(a)) - (-F(b))$

Men förenklar vi detta får vi bara

$-\int_b^a f(x) dx = F(b) - F(a)$

och därmed

$-\int_b^a f(x) dx = \int_a^b f(x) dx$

Rena matematiker anser nog att bevis med integralkalkylens fundamentalsats löper risk för att vara cirkulära men de är väldigt kraftfulla för att rimliggöra om en egenskap stämmer.