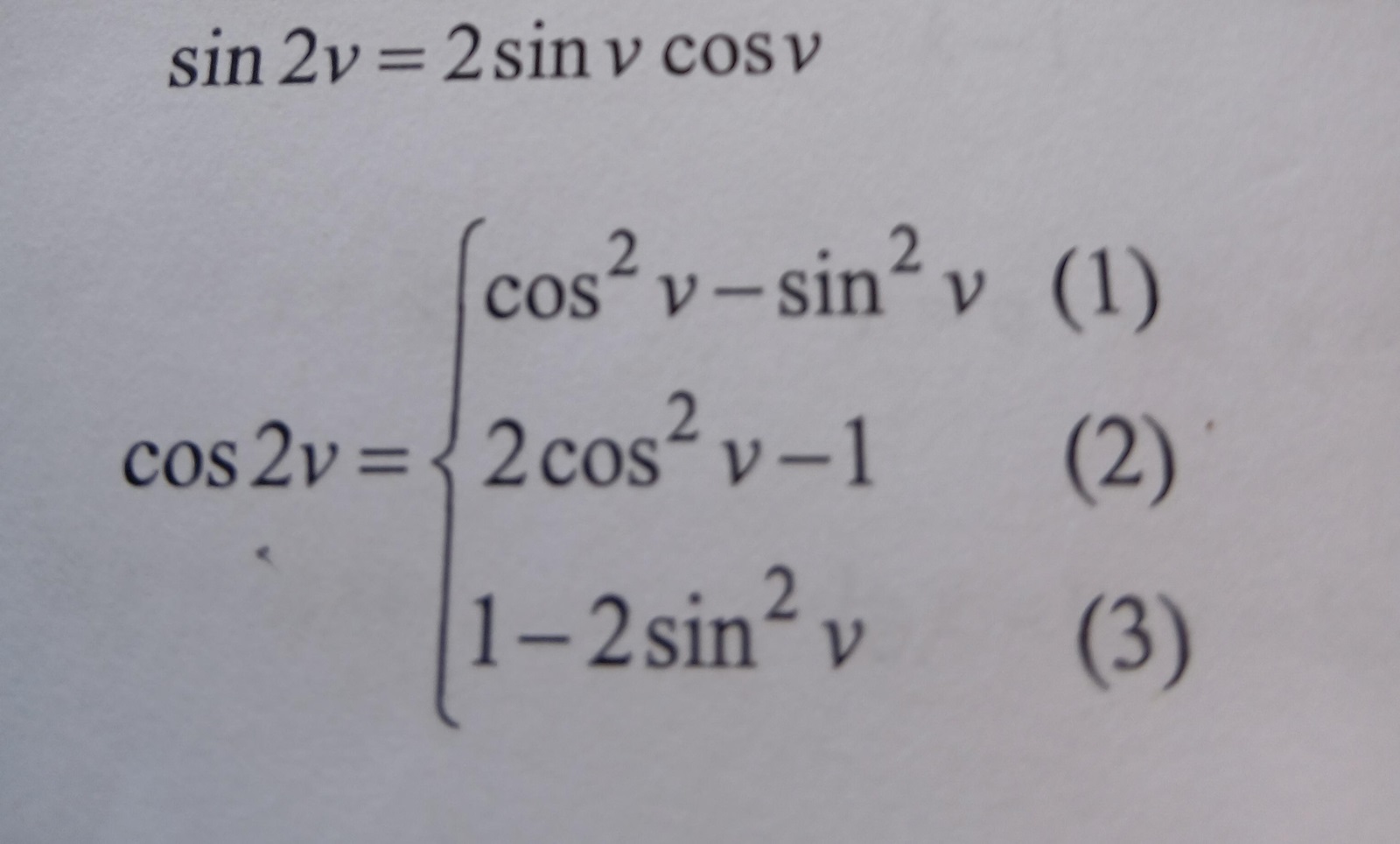Visa likheten

Har jsg gjort slarvfel på vägen ?

det går bra 

varför blev det fel ? Kunde man inte göra en U-substitiun ?

Det blir enklare att använda regeln: $2{\cos }^{2}x = 1+ \cos 2x$

Substitutionen blir fel eftersom man måste ändra integrationsgränserna och byta ut $dx$ mot $du$ som ofta inkluderar en extra faktor (intuitionen bakom det är att man ska "översätta" integralen så att den skrivs uttryckt i $u$ och inte i $x$). Exemplena som ges på wikipediaartikeln är ganska bra för att förstå hur man använder substitution. 

Sättet de vill att du ska lösa denna fråga är att använda en formel för dubbla vinkeln: $\cos 2x = 2\cos^2 x - 1$

jag har lite problem att beräkna$2\int \left({\cos }^2\right(x)-1) dx$

Du vill beräkna integralen av $2 \cos^2 x$.

Dubbla vinkelns formel säger att $\cos 2x = 2\cos^2 x - 1$, vilket medför att $2\cos^2 x = 1+\cos 2x$. Du behöver alltså integrera 1+cos(2x):

$\displaystyle \int_0^\pi 2 \cos^2 x\,dx = \int_0^\pi \left(1+\cos 2x\right)\,dx = \ldots$

Så här ?

Hänger fortfarnde inte med

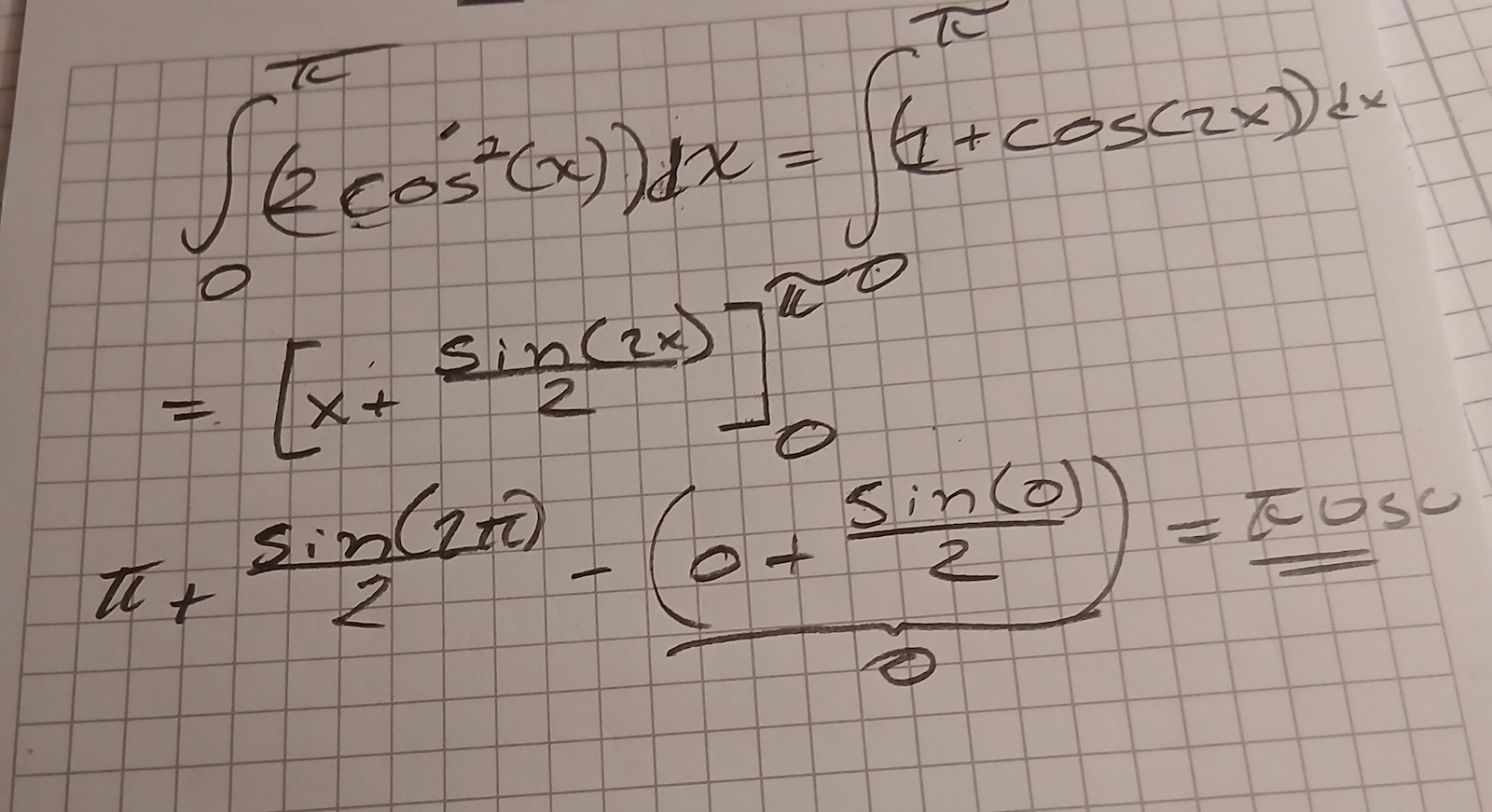
Jag undrar hur svaret blivit om man hade gjort U-substitution på korrekt sätt ?

Arup skrev:

Jag undrar hur svaret blivit om man hade gjort U-substitution på korrekt sätt ?

Ditt inlägg 10 ser bra ut.

Den substitution du försökte med fungerar inte på den här integralen. Jag föreslår att du väntar med variabelsubstitution i integraler till dess att du kommit till det avsnittet. Ingår det ens i gymnasiematten numera?