Visa med induktion att olikheten gäller...
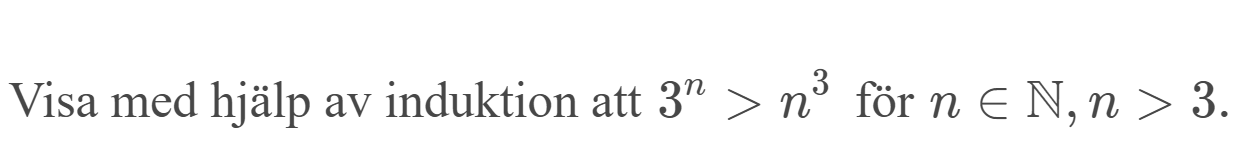
Jag har svårt att bevisa följande påstående och facits förklaring gör det inte enklare. Facit:

Jag förstår varför jag måste bevisa blå men inte röd. Dvs. varför visa med två på varandra följande heltal samt att 3 *VL för n= p+1 samt 3*Hö för n = p+1. Är det någon som skulle kunna förklara detta? Eller finns det möjligtvis en enklare metod? Kanske ansätta blå VL till f(p) och visa att för p=4 har funktionen sitt minsta värde (som är större än 0) och därefter växande för
Man kan absolut visa detta med att kolla på funktioner. Många olikheter kan visas på det sättet. Jag tycker inte facit har en särskilt bra lösning. En lösning jag tycker om (skippar basfallet)
Vi antar att vi har något heltal där olikheten gäller. Alltså har vi att
Nu vill vi visa att från detta antagande följer det att
Vi börjar med högerledet och idén är att vi ska göra det mindre och mindre, tills vi får vänsterledet.
Från antagandet har vi att
Härefter kan vi notera att eftersom kan vi göra uttrycket mindre genom att ersätta ett med 4. Detta ger oss att
.
Vi kan göra en liknande del där vi ersätter 2st med 4:
Nu kommer vi ihåg att
Och ersätter det andra med vår första olikhet och det tredje med vår andra olikhet, vilket gör uttrycket mindre.
Alltså är
och där är induktionssteget visat.
Jag försöker förstå din metod, jag har sett att andra använder s.k. "ersättningar". Men hur kan du t.ex. fram till att p^3 > 4p^2 för p>4?
Anonym_15 skrev:Jag försöker förstå din metod, jag har sett att andra använder s.k. "ersättningar". Men hur kan du t.ex. fram till att p^3 > 4p^2 för p>4?
Då p^2(p-4)>0 för p>4 har vi att p^3-4p2>0 för p>4 vilket ger p^3>4p2

