2
svar
130
visningar
Visa påståndet
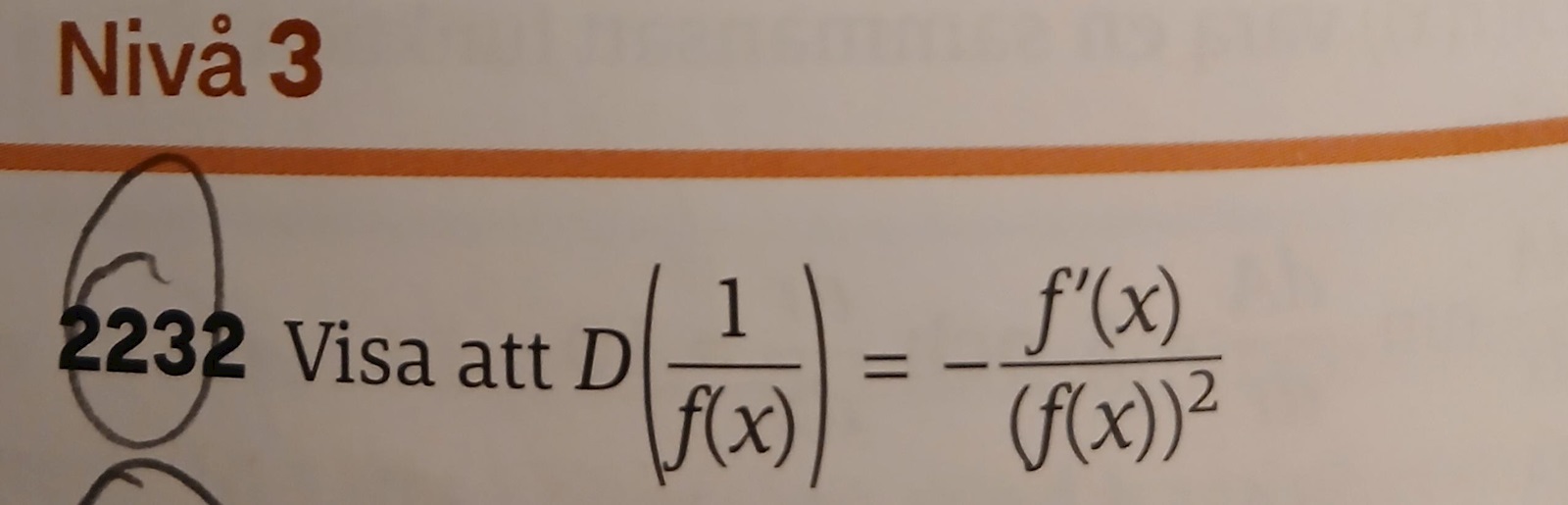
Jag tänker mig jag omskriver
sen tar jag dess derivata
Det är på god väg! När du deriverar, glöm inte kedjeregeln!
Borde inte vara så svårt att visa det utifrån derivatans definition.

