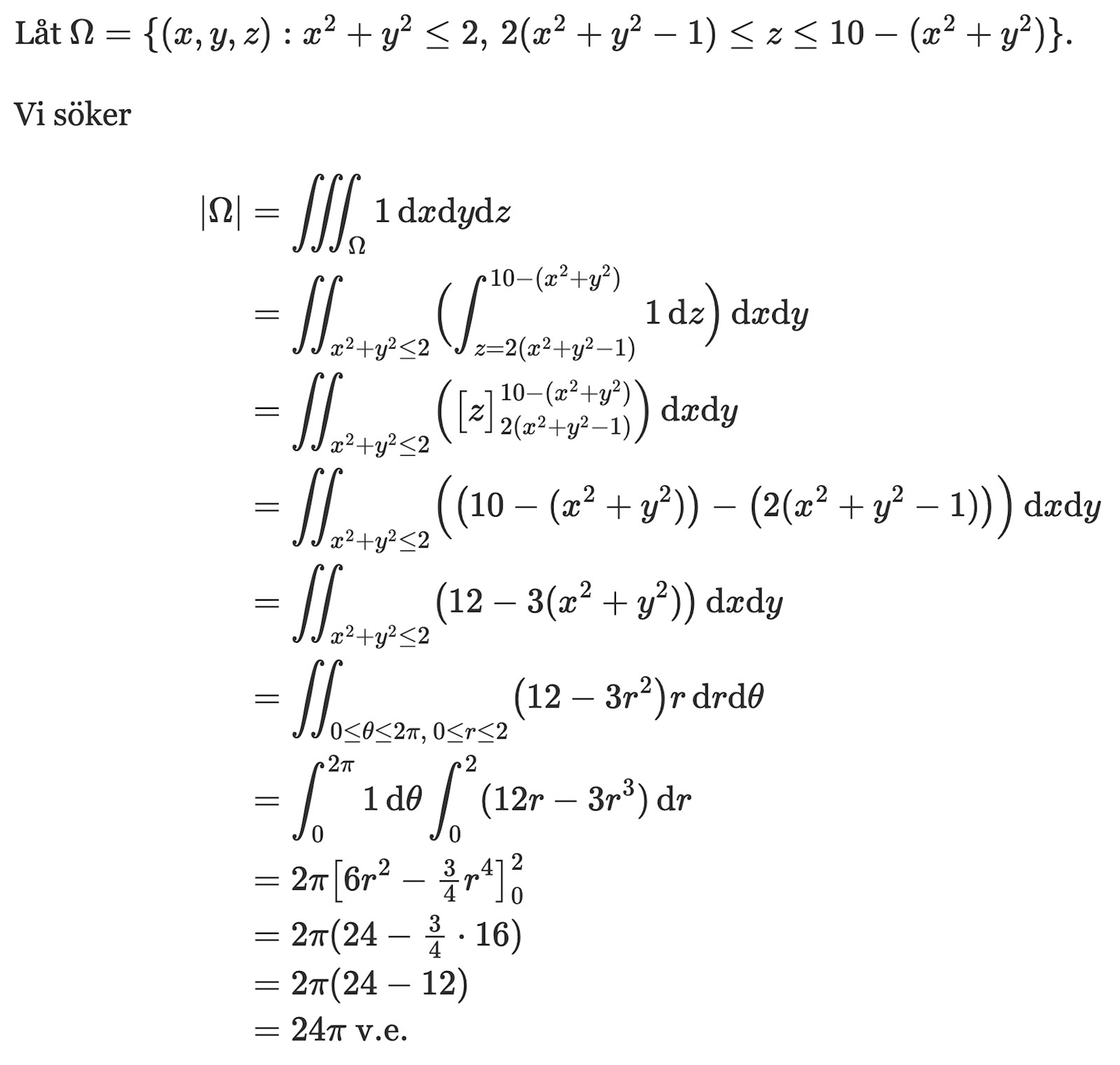Volym från trippelintegraler
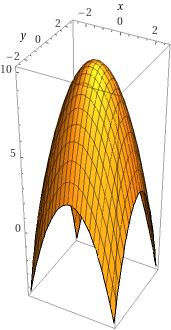
Försöker räkna ut volymen mellan z=10-x^2-y^2 och z=2(x^2+y^2-1). Försöker få fram de polära gränsvärdena. De jag fått fram är (< är oxå lika med, fanns inget kortkommando för de) 0<R<2. De andra antar jag är 0<θ<2pi och 0<Φ<pi. Svaret ska bli 24pi, men får till (8/3)2pi(1-1/sqrt2).
TECH_GUY skrev:Försöker räkna ut volymen mellan z=10-x^2-y^2 och z=2(x^2+y^2-1). Försöker få fram de polära gränsvärdena. De jag fått fram är (< är oxå lika med, fanns inget kortkommando för de) 0<R<2. De andra antar jag är 0<θ<2pi och 0<Φ<pi. Svaret ska bli 24pi, men får till (8/3)2pi(1-1/sqrt2).
Hur ser din (tredimensionella) figur ut? Försök rita en bild och lägg upp den!
Man använder ofta (t.ex. i programmeringsspråk) kombinationerna <= eller =< för "mindre än eller lika med" när man inte har tillgång till rätt tecken.
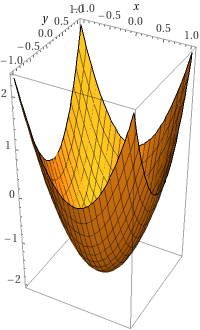Jag lyckades inte få dem i samma bild.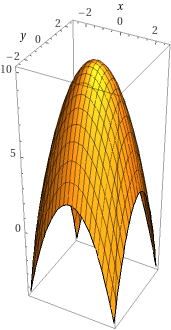 
Smaragdalena skrev:
Jag lyckades inte få dem i samma bild.
Jo jag, fick fram figurerna med och att de skär i r=2 måste stämma. Det jag funderar på är om θ ska vara 2pi. Den sträcker ju sig 360 grader så det antar jag. Samma med Φ, den borde vara pi. Har du någon tanke på hur man ska få till de?
Jag tror cylinderkoordinater är bättre än sfäriska.
Här är en liten bild som kanske hjälper
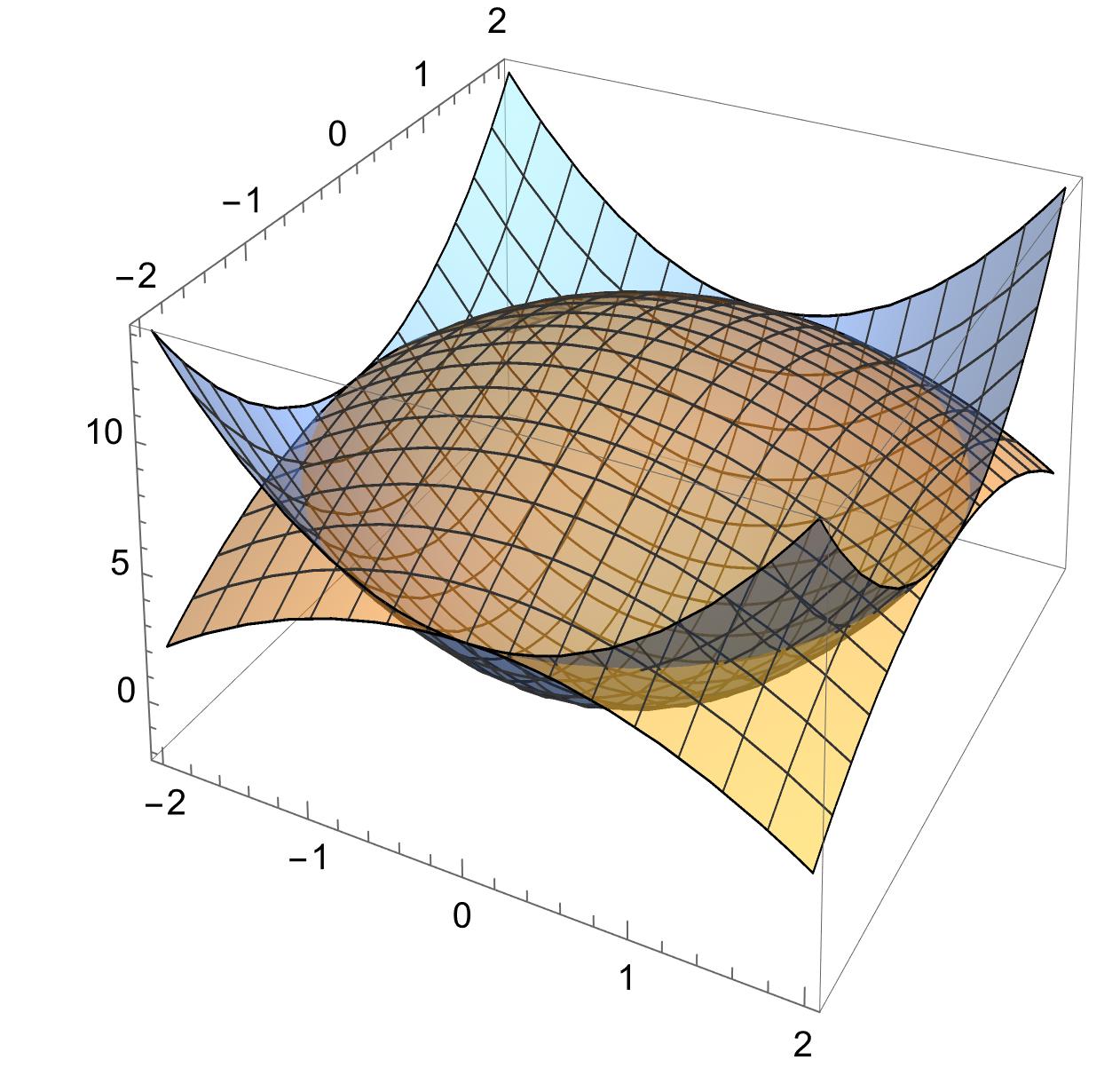
Laguna skrev:Jag tror cylinderkoordinater är bättre än sfäriska.
cylinderkoordinater kommer ju bli 0<R<2 , 0<θ<2pi , men den sista har jag svårt att se. Blir det ksk intervallet i Z-led?
Om du tänker dig en vertikal z-axel i min figur så funderar vi ut vilka höjder ytorna spänner över.
När ytorna skär varandra är radien 2. Jag tror du räknade ut det också. Det innebär att z=6.
Den undre ytan skär z-axeln när r=0 vilket ger z=-2
Den övre ytan skär z-axeln när r=0 vilket ger z=10
Vi vet nu at kroppen består av 2 kroppar (de har olika "krökning"), en kropp mellan [-2,6] och en mellan [6,10].
Om du integrerar resp. "delkropp" som cirkelskivor för z=-2...6 och z=6...10 får du volymen.
Den undre kroppen ger volymen 16π och den övre 8π, tillsammans 24π v.e.
Trinity2 skrev:Om du tänker dig en vertikal z-axel i min figur så funderar vi ut vilka höjder ytorna spänner över.
När ytorna skär varandra är radien 2. Jag tror du räknade ut det också. Det innebär att z=6.
Den undre ytan skär z-axeln när r=0 vilket ger z=-2
Den övre ytan skär z-axeln när r=0 vilket ger z=10
Vi vet nu at kroppen består av 2 kroppar (de har olika "krökning"), en kropp mellan [-2,6] och en mellan [6,10].
Om du integrerar resp. "delkropp" som cirkelskivor för z=-2...6 och z=6...10 får du volymen.
Den undre kroppen ger volymen 16π och den övre 8π, tillsammans 24π v.e.
Jo det resonemanget är ju helt rimligt och korrekt, skulle dock behöva använda den andra metoden med trippel integralerna......
TECH_GUY skrev:Trinity2 skrev:Om du tänker dig en vertikal z-axel i min figur så funderar vi ut vilka höjder ytorna spänner över.
När ytorna skär varandra är radien 2. Jag tror du räknade ut det också. Det innebär att z=6.
Den undre ytan skär z-axeln när r=0 vilket ger z=-2
Den övre ytan skär z-axeln när r=0 vilket ger z=10
Vi vet nu at kroppen består av 2 kroppar (de har olika "krökning"), en kropp mellan [-2,6] och en mellan [6,10].
Om du integrerar resp. "delkropp" som cirkelskivor för z=-2...6 och z=6...10 får du volymen.
Den undre kroppen ger volymen 16π och den övre 8π, tillsammans 24π v.e.
Jo det resonemanget är ju helt rimligt och korrekt, skulle dock behöva använda den andra metoden med trippel integralerna......
OK! Skall bara käka, så kommer en sådan lösning också.
Trinity2 skrev:TECH_GUY skrev:Trinity2 skrev:Om du tänker dig en vertikal z-axel i min figur så funderar vi ut vilka höjder ytorna spänner över.
När ytorna skär varandra är radien 2. Jag tror du räknade ut det också. Det innebär att z=6.
Den undre ytan skär z-axeln när r=0 vilket ger z=-2
Den övre ytan skär z-axeln när r=0 vilket ger z=10
Vi vet nu at kroppen består av 2 kroppar (de har olika "krökning"), en kropp mellan [-2,6] och en mellan [6,10].
Om du integrerar resp. "delkropp" som cirkelskivor för z=-2...6 och z=6...10 får du volymen.
Den undre kroppen ger volymen 16π och den övre 8π, tillsammans 24π v.e.
Jo det resonemanget är ju helt rimligt och korrekt, skulle dock behöva använda den andra metoden med trippel integralerna......
OK! Skall bara käka, så kommer en sådan lösning också.
Tack så mycket, hoppas det smakar!
Jag hjälpte till med ett liknande problem för ett tag sen. Titta på den lösningen så kanske det klarnar.
TECH_GUY skrev:Trinity2 skrev:TECH_GUY skrev:Trinity2 skrev:Om du tänker dig en vertikal z-axel i min figur så funderar vi ut vilka höjder ytorna spänner över.
När ytorna skär varandra är radien 2. Jag tror du räknade ut det också. Det innebär att z=6.
Den undre ytan skär z-axeln när r=0 vilket ger z=-2
Den övre ytan skär z-axeln när r=0 vilket ger z=10
Vi vet nu at kroppen består av 2 kroppar (de har olika "krökning"), en kropp mellan [-2,6] och en mellan [6,10].
Om du integrerar resp. "delkropp" som cirkelskivor för z=-2...6 och z=6...10 får du volymen.
Den undre kroppen ger volymen 16π och den övre 8π, tillsammans 24π v.e.
Jo det resonemanget är ju helt rimligt och korrekt, skulle dock behöva använda den andra metoden med trippel integralerna......
OK! Skall bara käka, så kommer en sådan lösning också.
Tack så mycket, hoppas det smakar!
Tackar! Man hade önskat man var lika bra på att fixa käk som man är på matte... :)
Här kommer en "klassisk integrallösning":
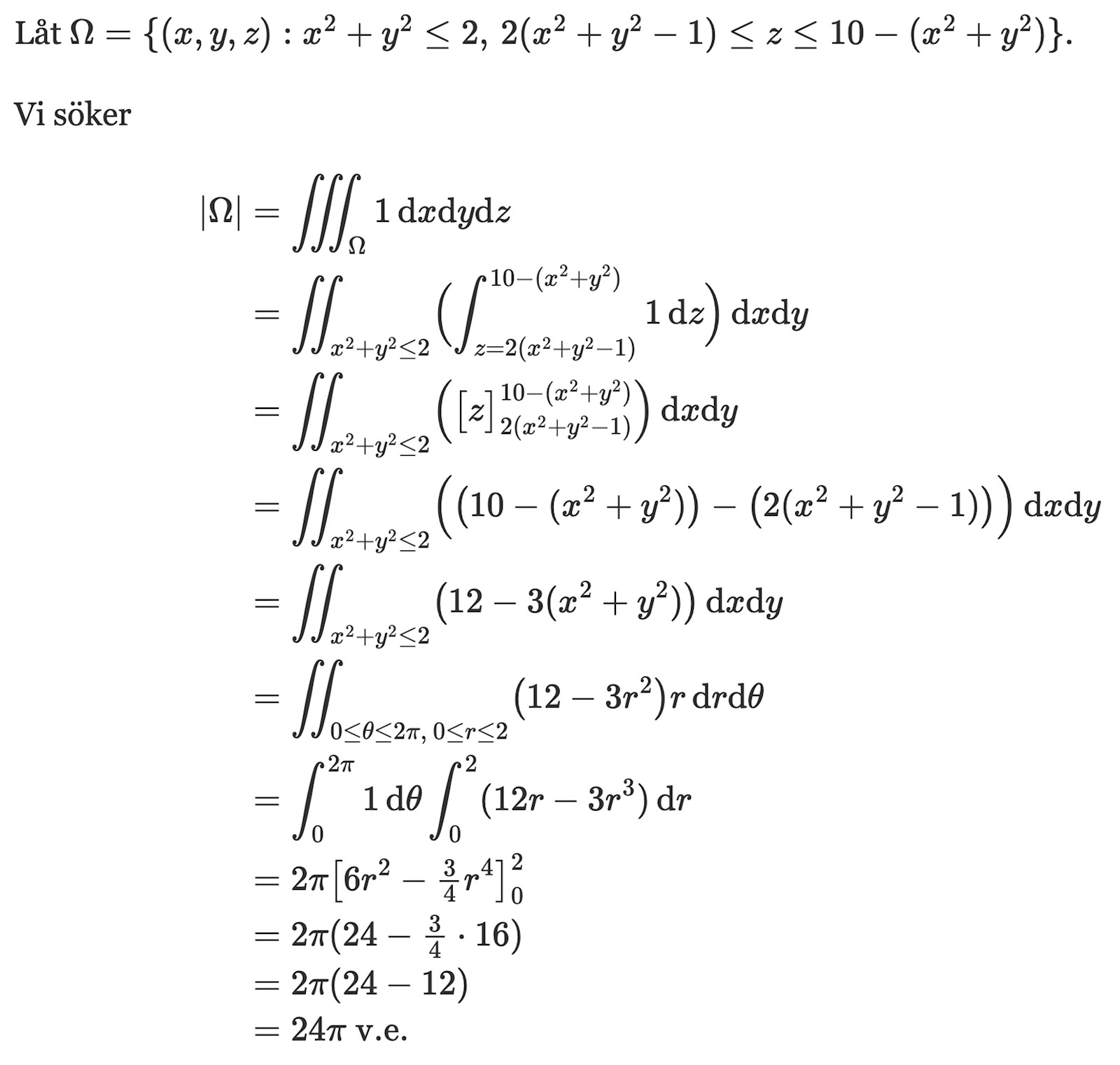
https://mathb.in/78372
Trinity2 skrev:TECH_GUY skrev:Trinity2 skrev:TECH_GUY skrev:Trinity2 skrev:Om du tänker dig en vertikal z-axel i min figur så funderar vi ut vilka höjder ytorna spänner över.
När ytorna skär varandra är radien 2. Jag tror du räknade ut det också. Det innebär att z=6.
Den undre ytan skär z-axeln när r=0 vilket ger z=-2
Den övre ytan skär z-axeln när r=0 vilket ger z=10
Vi vet nu at kroppen består av 2 kroppar (de har olika "krökning"), en kropp mellan [-2,6] och en mellan [6,10].
Om du integrerar resp. "delkropp" som cirkelskivor för z=-2...6 och z=6...10 får du volymen.
Den undre kroppen ger volymen 16π och den övre 8π, tillsammans 24π v.e.
Jo det resonemanget är ju helt rimligt och korrekt, skulle dock behöva använda den andra metoden med trippel integralerna......
OK! Skall bara käka, så kommer en sådan lösning också.
Tack så mycket, hoppas det smakar!
Tackar! Man hade önskat man var lika bra på att fixa käk som man är på matte... :)
Här kommer en "klassisk integrallösning":
https://mathb.in/78372
Tack! De va bussigt av dig! Ser vart jag tänkte fel, hade fått någon skum tanke om vad dz skulle ha för intervall.
