Volym med hjälp av integrering

Vilken form har varje skiva, som är vinkelrät  mot y-axeln?

Jag saknar ritmöjligheter så jag får försöka beskriva med ord. Projektionen av osten i xz-planet blir en rätvinklig triangel med kateterna r och h. Bestäm hypotenusans ekvation i detta plan. Skiva osten (mums!) i halvcirklar vinkelräta mot runda cylinderytan. Radien i dessa halvcirklar varierar från r till 0 och beror på höjden z och hypotenusans ekvation. Bestäm arean av halvcirklarna som funktion av höjden z. Integrera denna areafunktion från 0 till h. Hoppas någon annan har ritmöjligheter för jag tror det hjälper här.

Jag är inte med på det Tomten beskriver. så som jag ser det är det då bara en halvcirkel vid z = 0. Övriga skivor är cirkelsegment:

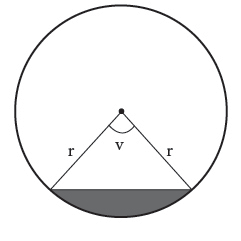
Här ges arean av segmentet i grått som:

$A_s = \dfrac{1}{2}r^2(v - \sin v)$

Radien är konstant men vinkeln varierar från $\pi$ till $0$. Volymen på alla skivor kan du sedan integrera fram genom att ta reda på hur vinkeln varierar med avseende på $z$.

Ledning:

$r\cos(v/2) = z\dfrac{r}{h}$

Tillägg: 21 nov 2021 05:01

Jag kan tycka att Smaragdalenas metod är bättre och enklare. Framförallt blir integralen på din nivå. 

Smaragdalena skrev:

Vilken form har varje skiva, som är vinkelrät  mot y-axeln?

Har väldigt svårt att förstå bilden men det borde väl bli ett cirkelsegment, eller?

Nej, varje skiva blir en rätvinklig triangel.

Om du tittar vinkelrätt mot x-z planet har du följande bild:

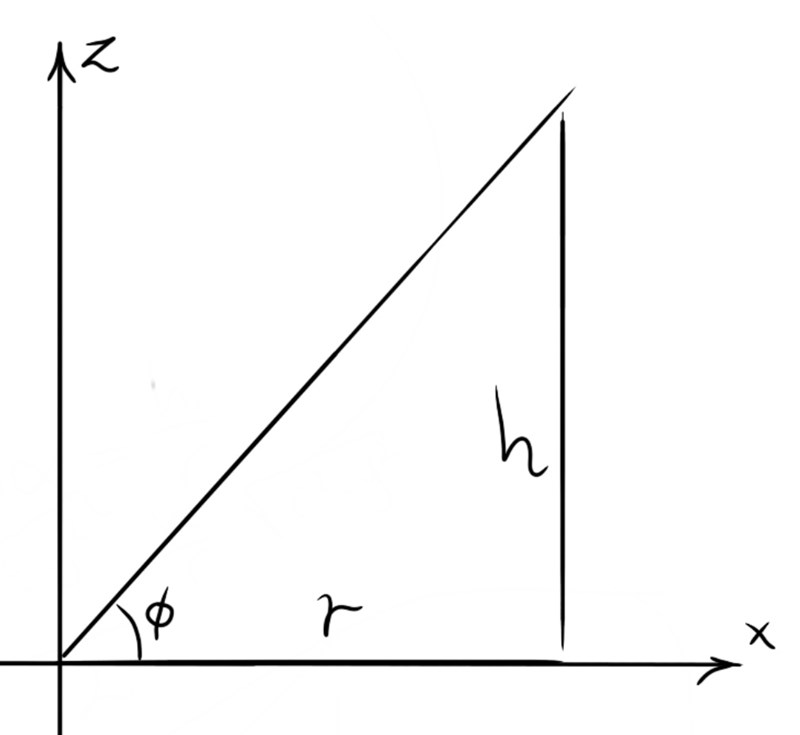
Alltså en rätvinklig triangel med kateterna $r$, $h$ och vinkeln $\tan(\phi) =h/r$. Vi ser att denna är en del av vår volym som:

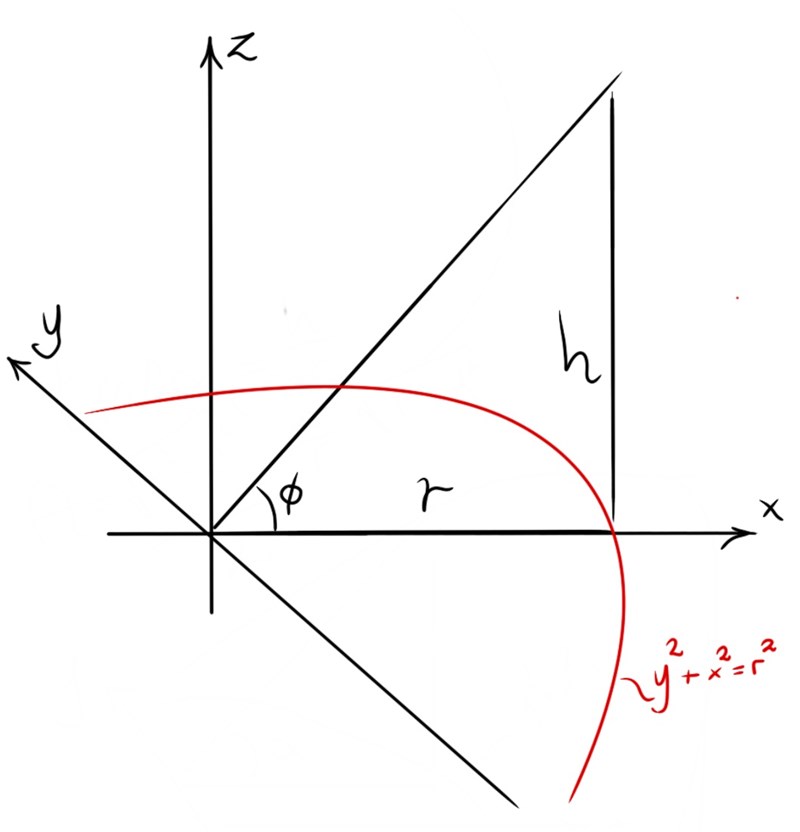
Där alltså nedre hörnet ligger på en cirkel med ekvationen $y^2+x^2=r^2$. Om vi nu tar en godtycklig skiva vid något $y$ mellan $+r$ och $-r$ har vi:

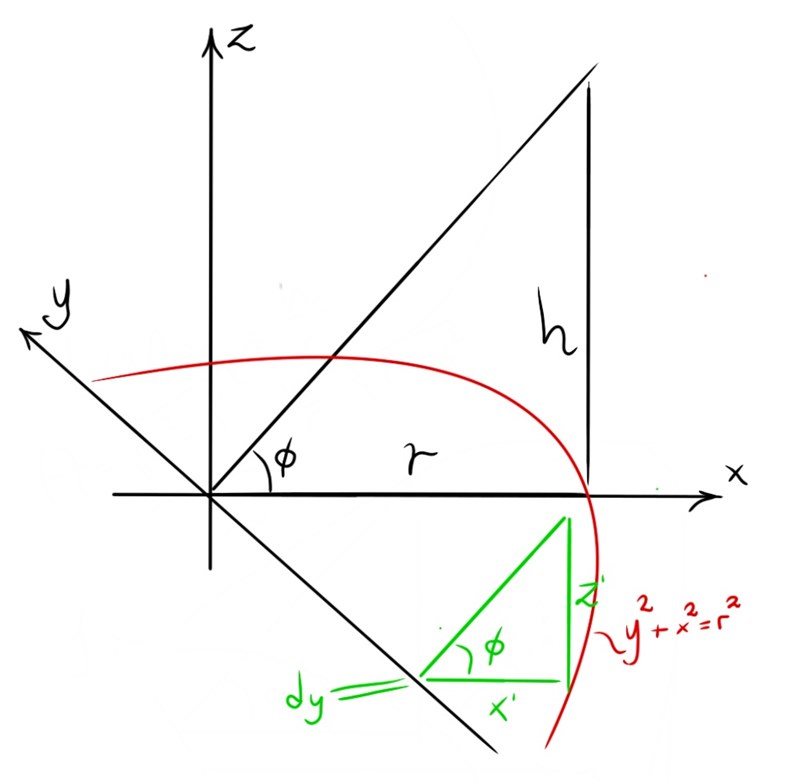
Där alltså triangelns kateter är:

$x' = \sqrt{r^2-y^2}$

$z' = x' \cdot \tan(\phi)$

Tjockleken på skivan sätter du som en infinitesimal $dy$ och differientialvolymen blir arean gånger $dy$. Dessa kan du sedan summera som en integral.

Om jag förstått dig rätt kan man sätta z' i en integral och få ut arean. Men vad är vinkeln ϕ? Hur kan man  ta reda på den?

Om du kollar längst upp i mitt inlägg ser du att jag skrev:

$\tan(\phi)=h/r$

Detta är alltså bara ett trigonometriskt samband. Annars kan du använda likformigheten mellan de mindre trianglarna och den med kateter $r$ och $h$. Det är ekvivalent (om de har samma vinkel är de likformiga).