Volym som beror av mer än en variabel

Tänker du kanske på rotationskroppar? Man kan beräkna volymen hos en kon med hjälp av dubbel- och trippelintegraler, men det är nog överkurs.

Teraeagle skrev:

Tänker du kanske på rotationskroppar? Man kan beräkna volymen hos en kon med hjälp av dubbel- och trippelintegraler, men det är nog överkurs.

 Nej, utan det är derivata man ska använda sig utav.

Tänker du på typ "maximera volymen av en läskburk, om materialåtgången ska vara max 40 kvadratcentimeter aluminium"? Liknande kan vara att bestämma de mått på en kon som ger den maximala volymen om summan av diametern och höjden för vara max en meter. Är det sådant du tänker på?

Smutstvätt skrev:

Tänker du på typ "maximera volymen av en läskburk, om materialåtgången ska vara max 40 kvadratcentimeter aluminium"? Liknande kan vara att bestämma de mått på en kon som ger den maximala volymen om summan av diametern och höjden för vara max en meter. Är det sådant du tänker på?

 Jaa! Precis! 

Att beräkna en volym med två variabler (som beror på varandra) är nästan samma sak som att beräkna en area som beror på två variabler:

https://www.pluggakuten.se/trad/nationella-prov-c-kursprov-ht-06-uppgift-18

> så var det kon det handlade om

(någon var snabbare) Basytans diameter plus höjd på en cirkulär kon är en meter. Bestäm konens form så att volymen blir som störst.

> maximera volymen av en läskburk, om materialåtgången ska vara 40 kvadratmeter

Då blir det ett klot !!!

Du kanske kan bevisa att en kvadrat är den variant av en rektangel som ger störst area ifall omkretsen ska vara konstant?

Kalla sidorna i rektangeln för x och y, arean för A och omkretsen för C. Visa att x=y ger störst area hos rektangeln och beräkna den största arean.

Det handlar inte riktigt om volymer, men var det något i den stilen som du tänkte dig?

Teraeagle skrev:

Du kanske kan bevisa att en kvadrat är den variant av en rektangel som ger störst area ifall omkretsen ska vara konstant?

Kalla sidorna i rektangeln för x och y, arean för A och omkretsen för C. Visa att x=y ger störst area hos rektangeln och beräkna den största arean.

Det handlar inte riktigt om volymer, men var det något i den stilen som du tänkte dig?

 Skulle du kunna förklara andra stycket?

Vilken del var oklar?

Du har en rektangel vars sidlängder är x och y.

Rektangeln har en konstant omkrets C, dvs oavsett hur du varierar värdena på x och y så är omkretsen alltid C.

Arean hos rektangeln motsvarar A.

I verkligheten skulle det kunna vara en bonde som ska sätta upp ett stängsel i formen av en rektangel för att skapa en inhängnad till sina får. Frågan är då hur stora sidorna ska vara för att ge en så stor inhängnad som möjligt eftersom det finns en begränsad mängd stängsel.

Teraeagle skrev:

Vilken del var oklar?

Du har en rektangel vars sidlängder är x och y.

Rektangeln har en konstant omkrets C, dvs oavsett hur du varierar värdena på x och y så är omkretsen alltid C.

Arean hos rektangeln motsvarar A.

I verkligheten skulle det kunna vara en bonde som ska sätta upp ett stängsel i formen av en rektangel för att skapa en inhängnad till sina får. Frågan är då hur stora sidorna ska vara för att ge en så stor inhängnad som möjligt eftersom det finns en begränsad mängd stängsel.

 Är det så du menar? Jag kommer inte vidare iallafall. Ska jag anta värden på x och y?

Du vet att arean är $A=x\cdot y$. Om du skall kunna derivera behöver du ett uttryck som bara beror på EN variabel, t ex x.

Du vet att omkretsen C=2x+2y. Använd detta för att ta fram y(x).

Smaragdalena skrev:

Du vet att arean är $A=x\cdot y$. Om du skall kunna derivera behöver du ett uttryck som bara beror på EN variabel, t ex x.

Du vet att omkretsen C=2x+2y. Använd detta för att ta fram y(x).

 Fast jag har fortfarande två variabler?

Soderstrom skrev:

Smaragdalena skrev:

Du vet att arean är $A=x\cdot y$. Om du skall kunna derivera behöver du ett uttryck som bara beror på EN variabel, t ex x.

Du vet att omkretsen C=2x+2y. Använd detta för att ta fram y(x).

 Fast jag har fortfarande två variabler?

 Nej, inte om du subtituerar in att $y=\frac{c-2x}{2}$, då har du bara kvar $x$ som variabel.

Smaragdalena skrev:

Soderstrom skrev:

Visa föregående citat

Smaragdalena skrev:

Du vet att arean är $A=x\cdot y$. Om du skall kunna derivera behöver du ett uttryck som bara beror på EN variabel, t ex x.

Du vet att omkretsen C=2x+2y. Använd detta för att ta fram y(x).

 Fast jag har fortfarande två variabler?

 Nej, inte om du subtituerar in att $y=\frac{c-2x}{2}$, då har du bara kvar $x$ som variabel.

 Ja. Det är jag med på, men konstanten C. Ska jag bara välja ett värde för den? 

Konstanten C har det konstanta värdet C. Det är ingen variabel.

Smaragdalena skrev:

Konstanten C har det konstanta värdet C. Det är ingen variabel.

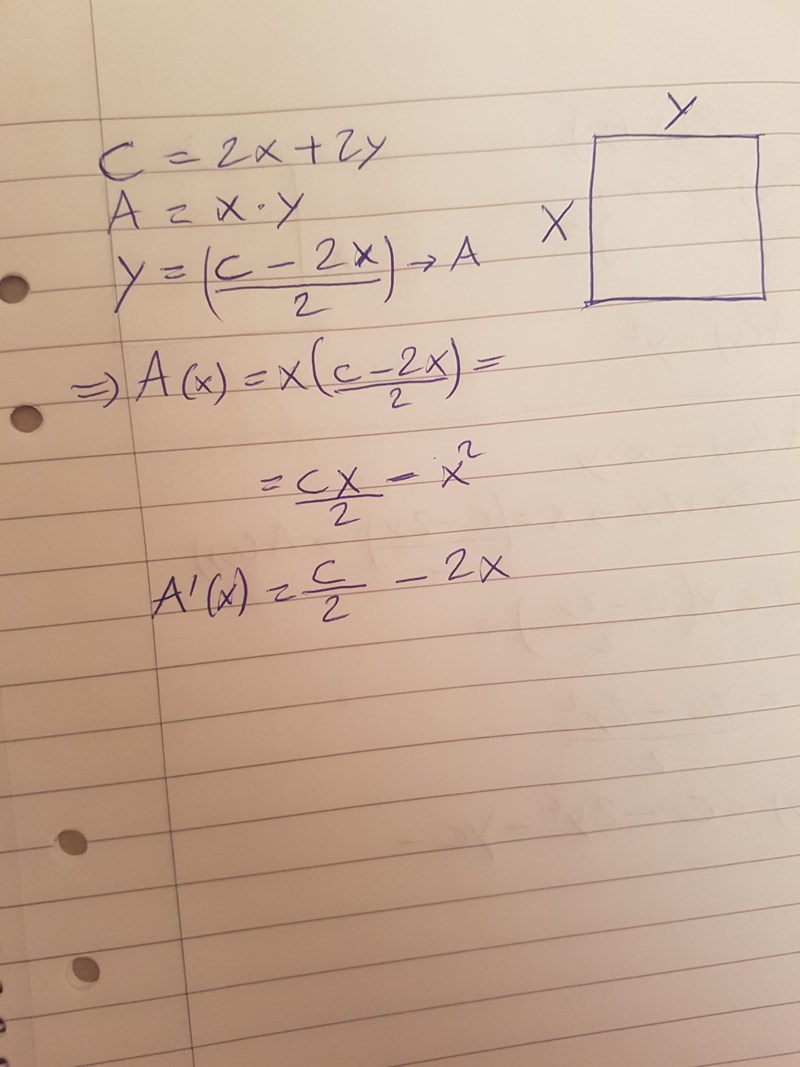 vad ska man göra nu? 

Vad gäller för A’(x) vid maximal area?

Teraeagle skrev:

Vad gäller för A’(x) vid maximal area?

 Ja. Derivatan ska vara lika med 0 för att ta reda på min.punkten eller max.punkten. sen löser jag x. Men sen?

Sedan beräknar du värdet på y. Vad kan du säga om x och y? Hur ska man välja dem för att få maximal area hos en rektangel? Hur stor blir den maximala arean uttryckt i C?

Teraeagle skrev:

Sedan beräknar du värdet på y. Vad kan du säga om x och y? Hur ska man välja dem för att få maximal area hos en rektangel? Hur stor blir den maximala arean uttryckt i C?

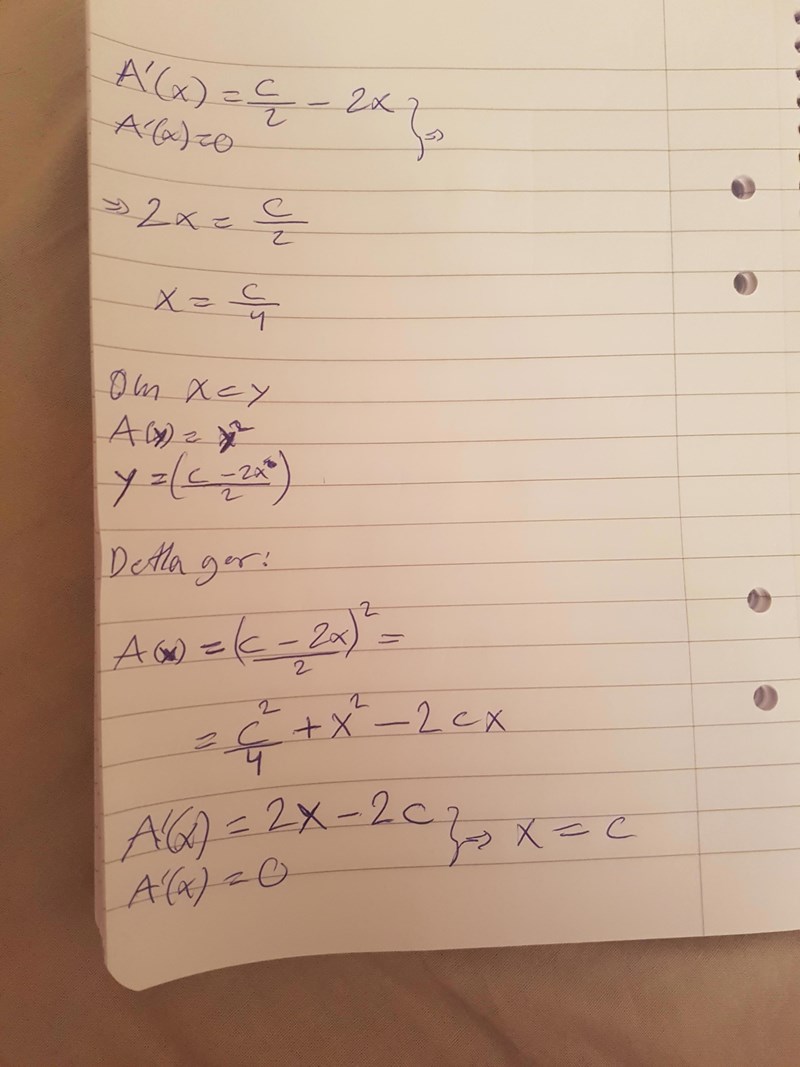
Jag har nog bevisat rätt. Men ändå är jag förvirrad. Varför måste vi ha med omkretsen? Är det bara för att reducera antalet variablar?

Du verkar (på ett otydligt sätt) visat att maximal area fås då x=y och att detta fås då x=C/4. Vad är då värdet på y uttryckt i C givet att y=(C-2x)/2? Maximala arean får du genom att multiplicera uttrycket för x med uttrycket för y. Omkretsen är med eftersom det är en konstant som begränsar arean. Om vi bara hade en rektangl med sidorna x och y så skulle den ju kunna ha hur stor area som helst ifall det inte fanns något som begränsade sidornas storlek.

Nej, en sida av rektangeln kan inte vara lika lång som hela rektangelns omkrets, det går inte ihop.

Du har kommit fram till att arean blir maximal om $x=\frac{C}{4}$.  Du vet sedan tidigare att $y=\frac{C-2x}{2}$. Sätt in uttrycket för $x$ i den formeln och beräkna $y$. Beräkna den maximala arean.

EDIT: Ändrade $c$ till $C$.

Jag hänger tyvärr inte med, vilket/vilka uttryck är det? 

Sätt in $x=\frac{C}{4}$ uttrycket $y=\frac{C-2x}{2}$. vad får du för uttryck för $y$? Sätt in detta och $x=\frac{C}{4}$ i  $Arean=x\cdot y$.

Smaragdalena skrev:

Sätt in $x=\frac{C}{4}$ uttrycket $y=\frac{C-2x}{2}$. vad får du för uttryck för $y$? Sätt in detta och $x=\frac{C}{4}$ i  $Arean=x\cdot y$.

 Ja, då för jag, $A=\frac{c^2}{16}$, men förstår fortfarande inte vad detta kan innebära. Jag måste nog börja om.

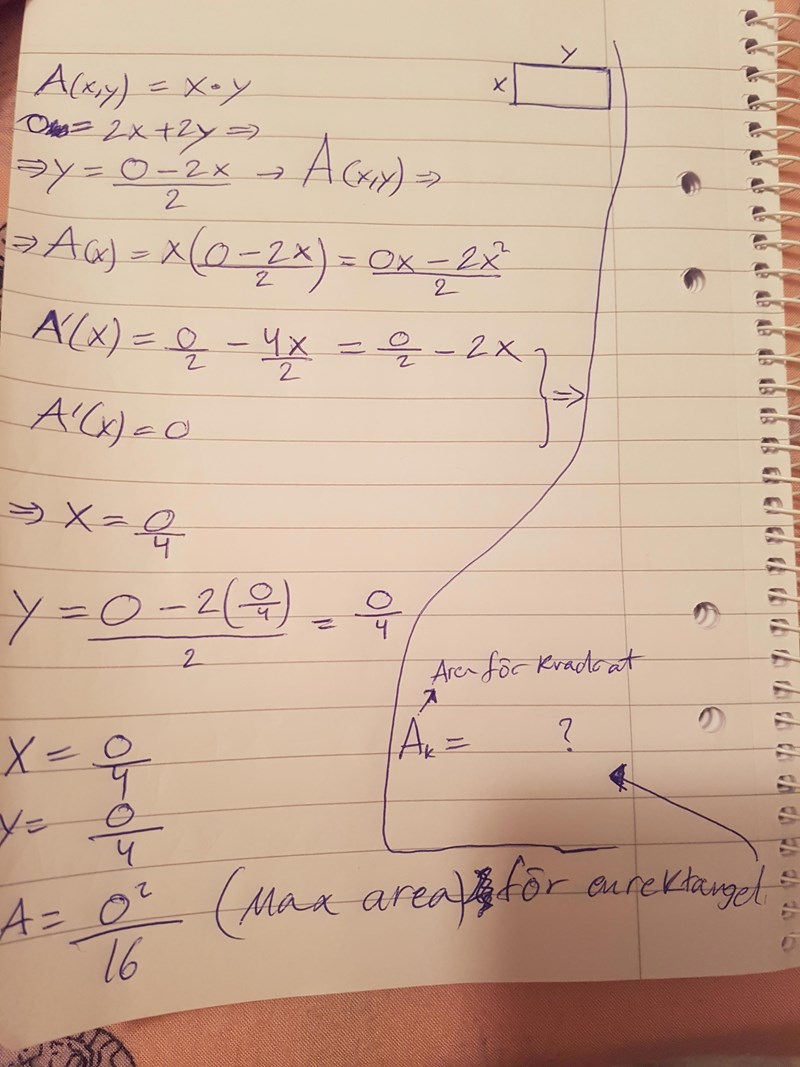
Vad har bevisat ens? Det jag skulle göra från början var att bevisa att en kvadrat har större area än en rektangel.

Teraeagle skrev:

Du kanske kan bevisa att en kvadrat är den variant av en rektangel som ger störst area ifall omkretsen ska vara konstant?

Kalla sidorna i rektangeln för x och y, arean för A och omkretsen för C. Visa att x=y ger störst area hos rektangeln och beräkna den största arean.

Det handlar inte riktigt om volymer, men var det något i den stilen som du tänkte dig?

Teraeagle skrev:

Teraeagle skrev:

Du kanske kan bevisa att en kvadrat är den variant av en rektangel som ger störst area ifall omkretsen ska vara konstant?

Kalla sidorna i rektangeln för x och y, arean för A och omkretsen för C. Visa att x=y ger störst area hos rektangeln och beräkna den största arean.

Det handlar inte riktigt om volymer, men var det något i den stilen som du tänkte dig?

 Okej! Men en fråga hur kan jag bevisa att tex en kvadrat har större area än en rektangel ifall omkretsen är konstant då?

Du har visat att maximal area fås när sidan x har längden C/4. Det innebär att y också har längden C/4. När sidorna i en rektangel är lika stora kallas den för kvadrat. En kvadrat är alltså den typ av rektangel som ger störst area, motsvarande C^2/16. Det du däremot måste göra i din lösning är att visa att du verkligen har hittat en maxpunkt hos arean, dvs gör en teckenstudie eller kolla tecknet hos andraderivatan.