Volymberäkning rotationskropp, kvadrat
Hej!
Undrar över en detalj i lösningen till denna uppgift.
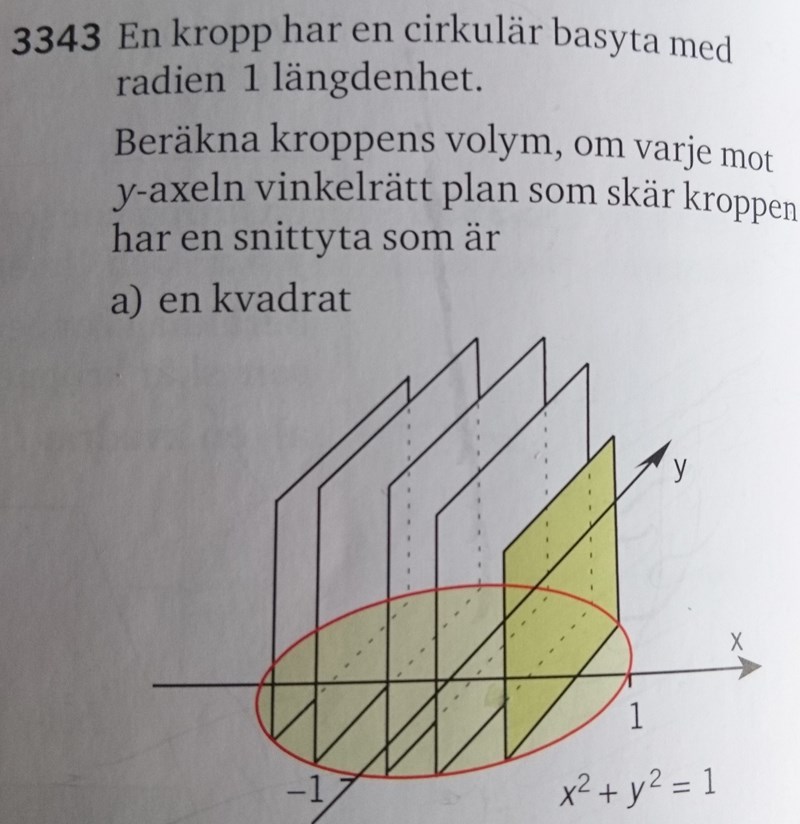
I facit står att en sida är 2y lång. Varför? Jag tycker att den är y lång. Var kommer 2 ifrån?
Jag förstår att den är y lång över x-axeln, -y lång under x-axeln, så totalt är den y+|-y| = 2y lång. MEN den ska ju rotera runt x-axeln, och då räknar vi väl bara med y-värdet i första och andra kvadranten (d.v.s. ovanför x-axeln)? Om längden 2y roterar blir den ju totalt 4 y lång.
Faxxi skrev:Hej!
Undrar över en detalj i lösningen till denna uppgift.
I facit står att en sida är 2y lång. Varför? Jag tycker att den är y lång. Var kommer 2 ifrån?
Jag förstår att den är y lång över x-axeln, -y lång under x-axeln, så totalt är den y+|-y| = 2y lång. MEN den ska ju rotera runt x-axeln, och då räknar vi väl bara med y-värdet i första och andra kvadranten (d.v.s. ovanför x-axeln)? Om längden 2y roterar blir den ju totalt 4 y lång.
Nej det står inte att den ska rotera.
Kroppen är redan bestämd av beskrivningen.
Den ser ut som en cylinder som står i xy-planet, där någon har rundat av toppen i positiv och negativ x-led.
Aha - nej, ska den inte rotera är det ju en annan sak. Men man kan alltså använda samma metod som för rotering, fast med någon modifikation ...?
Faxxi skrev:Aha - nej, ska den inte rotera är det ju en annan sak. Men man kan alltså använda samma metod som för rotering, fast med någon modifikation ...?
Ja. Kan du klura ut hur själv?
Den enda skillnaden mot min uträkning var att längden/höjden var just 2y istället för y. Den direkta slutsatsen blir väl något luddigt om "för dx gäller fördubbling av y" och motsvarande borde gälla för dy. Men jag har lite svårt att föreställa mig alla möjliga fall, så jag vet inte hur jag ska definiera det mer specifikt.
Du behöver ställa upp en integral och beräkna den.
Faxxi skrev:Den enda skillnaden mot min uträkning var att längden/höjden var just 2y istället för y. Den direkta slutsatsen blir väl något luddigt om "för dx gäller fördubbling av y" och motsvarande borde gälla för dy. Men jag har lite svårt att föreställa mig alla möjliga fall, så jag vet inte hur jag ska definiera det mer specifikt.
Skillnaden mot rotationskroppar är att skivorna här är kvadratiska och inte cirkulära.
Dela alltså in kroppen i jättemånga skivor som alla är kvadratiska.
Fyll i tomrummen i nedanstående lösningsförslag:
- En skiva vid ...-koordinaten ... har arean ... och tjockleken ...
- Alltså är den totala volymen integralen av ... från ... till ...
Ja, jag fick rätt svar ovan när jag ändrade från y till 2y. Jag gör på samma sätt även för b-delen i samma uppgift, men får ändå fel på "en detalj".
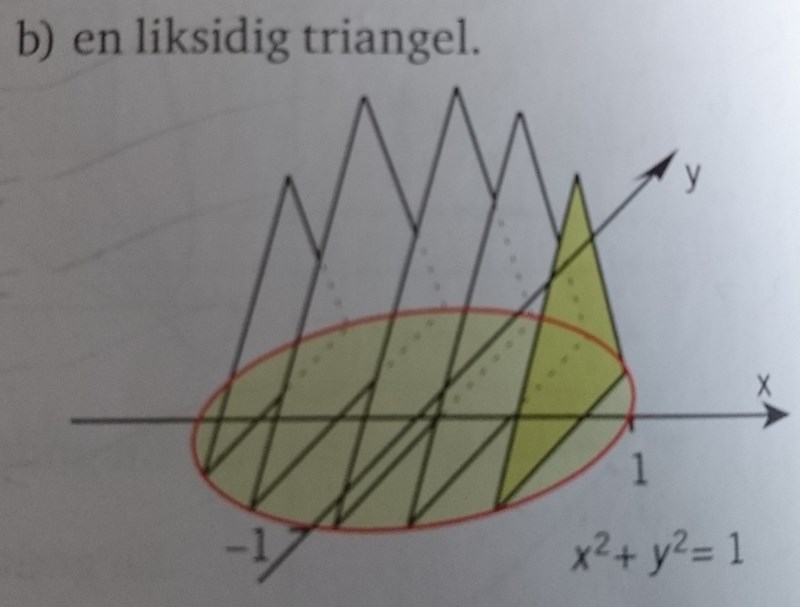
Min lösning: Arean A(x) ges av .
Pythagoras sats ger att . Basen ges av figuren: .
Då blir volymen .
Men enligt facit gäller .
Varför får jag ett y för mycket i min integral?
Faxxi skrev:Ja, jag fick rätt svar ovan när jag ändrade från y till 2y. Jag gör på samma sätt även för b-delen i samma uppgift, men får ändå fel på "en detalj".
Min lösning: Arean A(x) ges av .
Pythagoras sats ger att . Basen ges av figuren: .
Då blir volymen .
Men enligt facit gäller .
Varför får jag ett y för mycket i min integral?
Är du säker på att det står så i facit? Dels är det fel, dels så måste y uttryckas i termer av x för att integralen ska kunna beräknas.
Jag tycker att din integral ser rätt ut, men du är som sagt inte klar än.
Hur löste du a-uppgiften och vad fick du för svar där?
------------
Tips: för att förenkla integralberäkningen kan du utnyttja figurens symmetrier så att du endast behöver integrera från 0 till 1
------------
EDIT: Dessutom är uppgiften felformulerad alternativt figurerna felritade. De utritade planen är vinkelräta mot x-axeln, inte mot y-axeln som det står.



